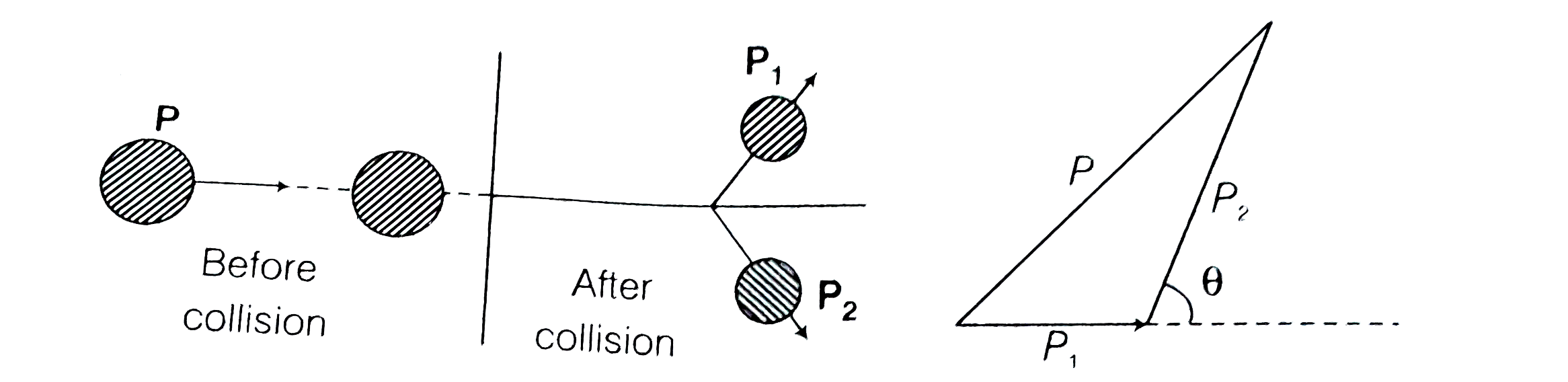Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball of mass mm, moving with a speed 2upsilon(0), collides inelastic...
Text Solution
|
- A billiard ball moving with a speed of 5 m//s collides with an identic...
Text Solution
|
- A ball of mass m m , moving with a speed 2upsilon(0) , collides inelas...
Text Solution
|
- A ball of mass m moving with a velocity v undergoes an oblique elastic...
Text Solution
|
- A ball of mass m moving with a speed 2v0 collides head-on with an iden...
Text Solution
|
- A ball moving with speed u collides with an identical ball at rest. Th...
Text Solution
|
- नियत वेग u से गतिमान m द्रव्यमान की एक गेंद एक अन्य ऐसी गेंद से टकराती...
Text Solution
|
- A ball of mass mm, moving with a speed 2upsilon(0), collides inelastic...
Text Solution
|
- A ball of mass m , moving with a speed 2v(0) collides inelastically ( ...
Text Solution
|