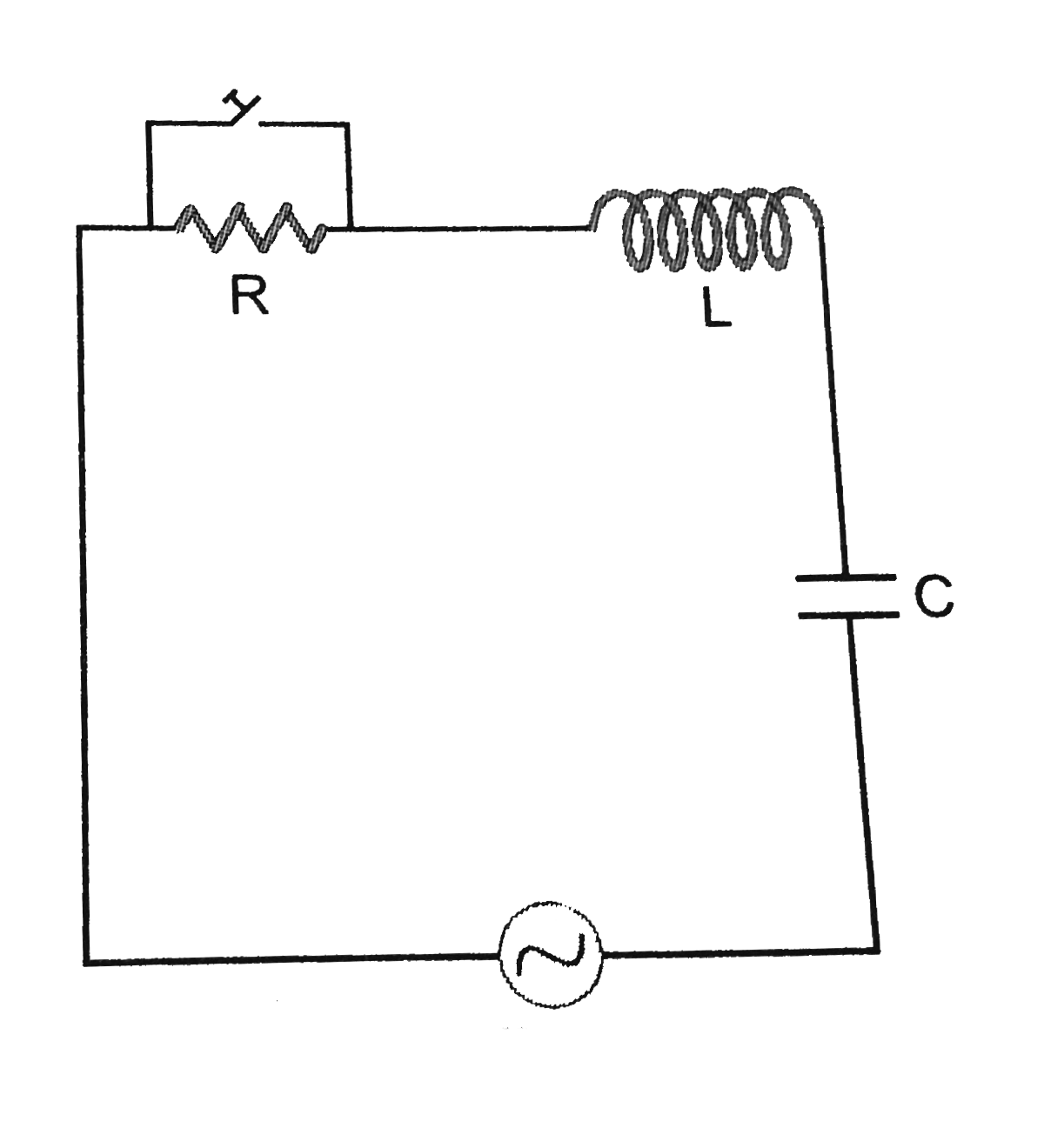
In the LCR circuit shown in Fig., the ac driving voltage is `upsilon = upsilon_(m) sin omega t`.
(i) Write down the equation of motion for q (t).
(ii) At `t = t_(0)`, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.
In the LCR circuit shown in Fig., the ac driving voltage is `upsilon = upsilon_(m) sin omega t`.
(i) Write down the equation of motion for q (t).
(ii) At `t = t_(0)`, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.

(i) Write down the equation of motion for q (t).
(ii) At `t = t_(0)`, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.

Text Solution
Verified by Experts
The correct Answer is:
A
Consider the R-L-C circuit shown in the adjacent diagram.
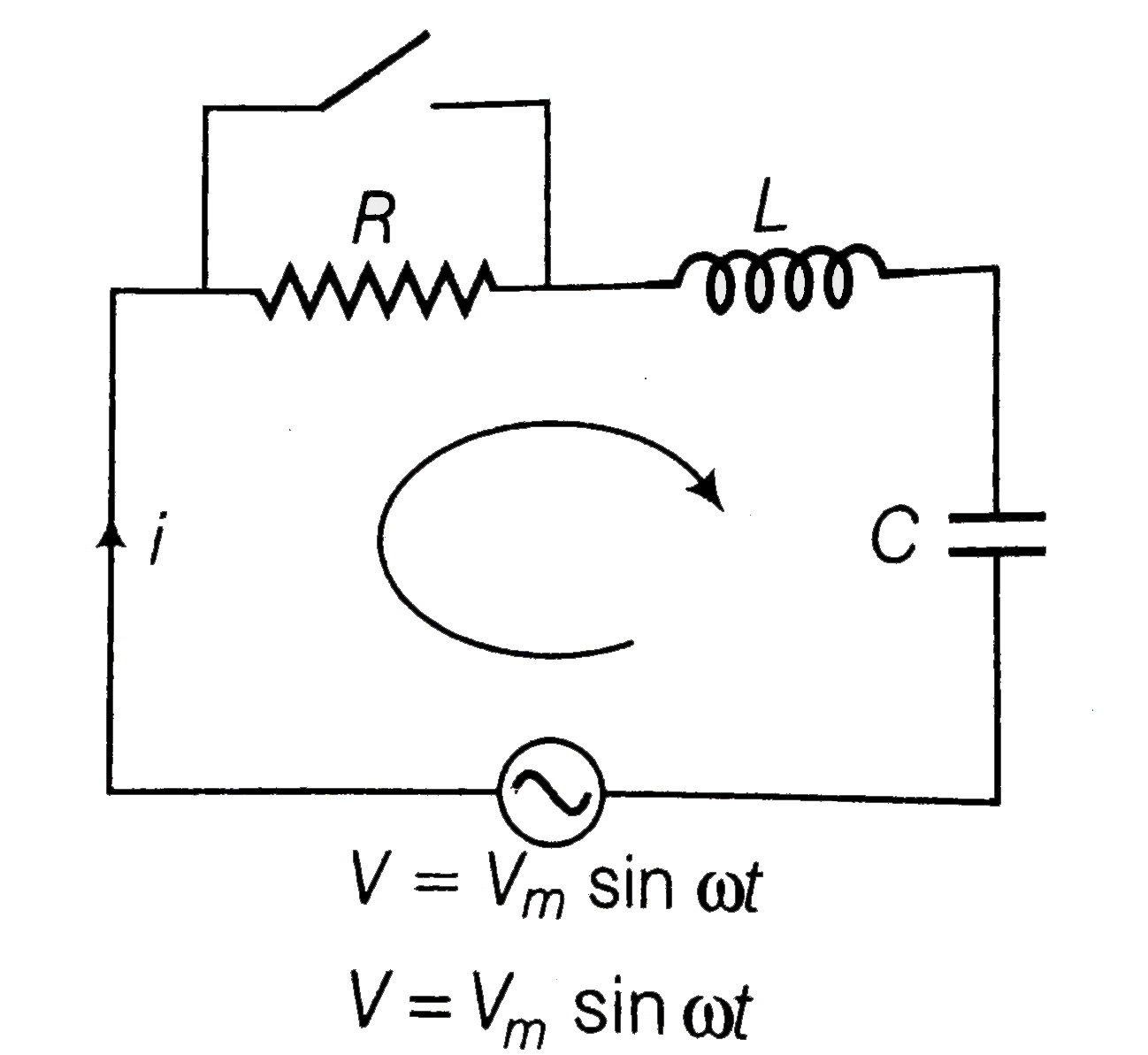
Given,
Let current at any instant be I
Applying KVL in the given circuit
`iR + L(di)/(dt) + q/C -V_(m) sinomegat=0`……….(i)
Now, we can write `i=(dq)/(dt) rArr (di)/(dt) = (d^(2)q)/(dt)^(2)`
From Eq. (i) `(dq)/(dt)R + L(d^(2)q)/(dt)^(2) + q/C=V_(m)sinomegat`
`rArr L(d^(2)q)/(dt)^(2)+ R(dq)/(dt)+ q/C=V_(m) sin omegat`
This is the required equation of variation (motion) of charge.
b) Let `q=q_(m)sin(omegat +phi)=-q_(m)cos(omegat + phi)`
`i=i_(m)sin(omegat+phi) = q_(m)omegasin(omegat+phi)`
`i_(m) = V_(m)/Z= V_(m)/(sqrt(R^(2)+(X_(C)-X_(L))^(2)`
`phi = tan^(-1)(X_(c)-X_(L))/R`
Where R is short circuited at `t=t_(0)`, energy is stored in L and C.
`U_(L) = 1/2Li^(2)=1/2LV_(m)/(sqrt(R^(2)+(X_(C)-X_(L)))^(2)] sin^(2)(omegat_(0)+phi)`
and `U_(C) = 1/2 xx q^(2)/C= 1/(2C)[q^(2)mcos^(2)(omegat_(0)+ phi)]`
`=1/(2C)[V_(m)/sqrt(R^(2)+(X_(C)-X_(L))^(2))^(2)]`
`=1/(2C) xx (i_(m)/omega)^(2) cos^(2)(omegat_(0) + phi)`
`=(i^(2)m)/(2Comega^(2))cos^(2)(omegat_(0)+phi)` `(therefore i_(m) = q_(m)omega`]
`=1/(2C) [V_(m)/(sqrt(R^(2)+(X_(C)-X_(L))^(2))^(2)]] (cos^(2)(omegat_(0)+phi)`
c) When R is a short circuited, the circuit becomes an L-C oscillaor. The capacitor will go on discharging and all energy will go to L and back and forth. Hence, there is oscillation of energy from electrostatic to magnetic and magnetic to electrostatic.
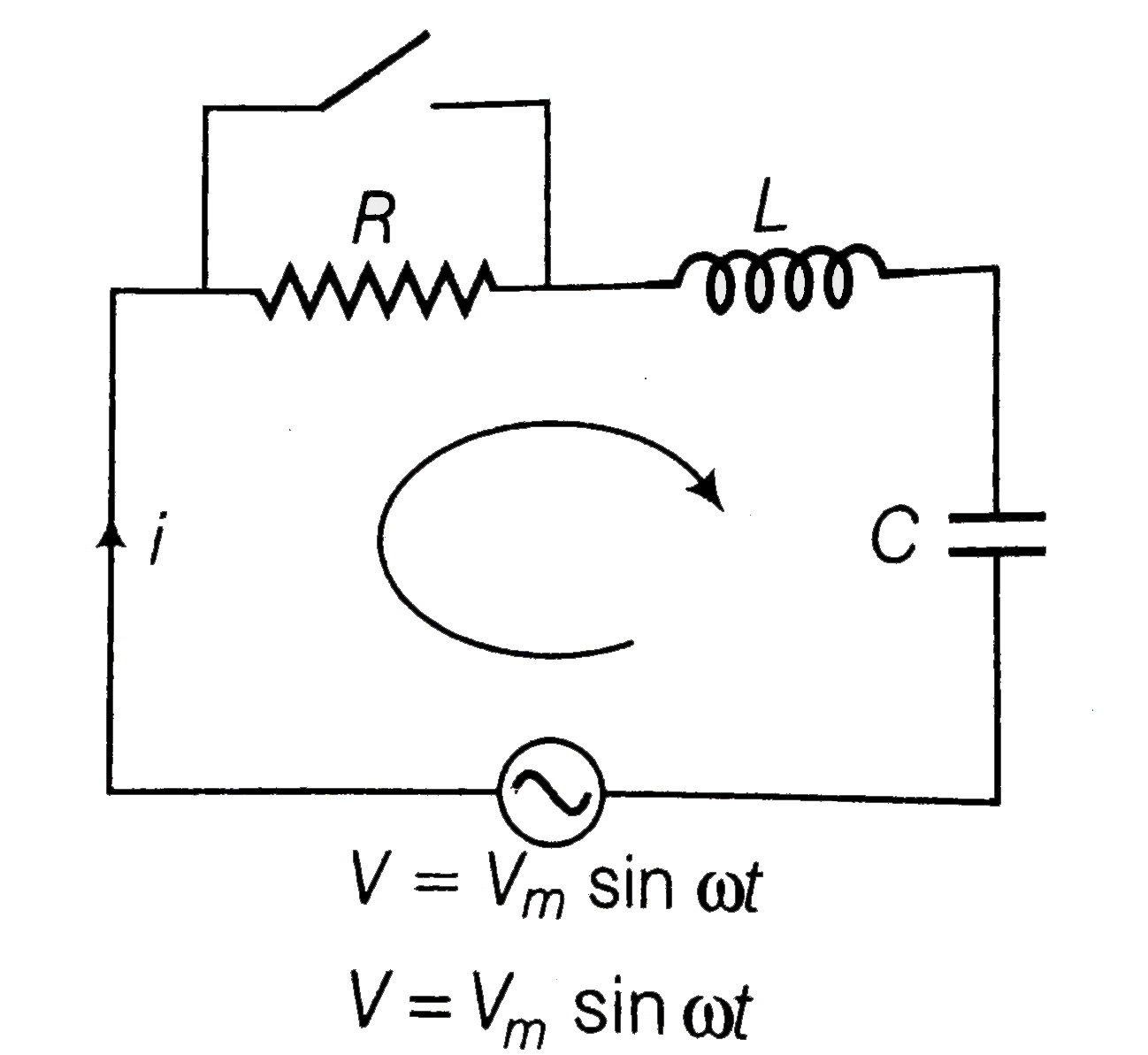
Given,
Let current at any instant be I
Applying KVL in the given circuit
`iR + L(di)/(dt) + q/C -V_(m) sinomegat=0`……….(i)
Now, we can write `i=(dq)/(dt) rArr (di)/(dt) = (d^(2)q)/(dt)^(2)`
From Eq. (i) `(dq)/(dt)R + L(d^(2)q)/(dt)^(2) + q/C=V_(m)sinomegat`
`rArr L(d^(2)q)/(dt)^(2)+ R(dq)/(dt)+ q/C=V_(m) sin omegat`
This is the required equation of variation (motion) of charge.
b) Let `q=q_(m)sin(omegat +phi)=-q_(m)cos(omegat + phi)`
`i=i_(m)sin(omegat+phi) = q_(m)omegasin(omegat+phi)`
`i_(m) = V_(m)/Z= V_(m)/(sqrt(R^(2)+(X_(C)-X_(L))^(2)`
`phi = tan^(-1)(X_(c)-X_(L))/R`
Where R is short circuited at `t=t_(0)`, energy is stored in L and C.
`U_(L) = 1/2Li^(2)=1/2LV_(m)/(sqrt(R^(2)+(X_(C)-X_(L)))^(2)] sin^(2)(omegat_(0)+phi)`
and `U_(C) = 1/2 xx q^(2)/C= 1/(2C)[q^(2)mcos^(2)(omegat_(0)+ phi)]`
`=1/(2C)[V_(m)/sqrt(R^(2)+(X_(C)-X_(L))^(2))^(2)]`
`=1/(2C) xx (i_(m)/omega)^(2) cos^(2)(omegat_(0) + phi)`
`=(i^(2)m)/(2Comega^(2))cos^(2)(omegat_(0)+phi)` `(therefore i_(m) = q_(m)omega`]
`=1/(2C) [V_(m)/(sqrt(R^(2)+(X_(C)-X_(L))^(2))^(2)]] (cos^(2)(omegat_(0)+phi)`
c) When R is a short circuited, the circuit becomes an L-C oscillaor. The capacitor will go on discharging and all energy will go to L and back and forth. Hence, there is oscillation of energy from electrostatic to magnetic and magnetic to electrostatic.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A series R-L circuit is subjected to an alternating voltage given as (v = v_0 sin omega t) . Then the variation of peak current (i) with frequency (v) is denoted by
For an LCR circuit driven at frequency omega , the equation reads L (di)/(dt) + Ri + (q)/(C ) = upsilon_(i) = upsilon_(m) sin omega t (i) Multiply the equation by I and simplify where possible. (ii) Interpret each term physically. (iii) Cast the equation in the form of a conservation of energy statement. (iv) Intergrate the equation over one cycle to find that the phase difference between upsilon and i must be acute.
In the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC . Find the current through the resistence R as a function of time t . After time t = 4 ms, the switch is connected in the position AC . Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C . At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L = 2 xx 10^(-4)H, C = 5 mF, R = (In 2)/(10) Omega and emf of the battery = 1 V .
In the circuit shown in Fig. the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega . At time t = 0 , the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m , while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm . the distance c is 5.0 cm . (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The current in the circuit 200 ms after closing S is
In the circuit shown in Fig. the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega . At time t = 0 , the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m , while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm . the distance c is 5.0 cm . (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The direction of current in the smaller circuit is
In the circuit shown in Fig. the capacitor has capacitance C = 20 muF and is initially charged to 100 V with the polarity shown. The resistor R_(0) has resistance 10 Omega . At time t = 0 , the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0 Omega m^(-1) and contains 25 loops. the larger circuit is a rectangle 2.0 m by 4.0 m , while the smaller one has dimensions a = 10.0 cm and b = 20.0 cm . the distance c is 5.0 cm . (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it. The curent in the smaller circuit 200 mus after closing S is
An ac source of voltage V=V_(m)sin omega t is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
In the series L-C-R circuit shown in the figure, the rms voltage across the resistor and inductor are 400 V and 700 V respectively. If the applied voltage is E=500sqrt(2)sin(omega t) , then the peak voltage across the capacitor is
In a series LCR circuit connected to an ac source of variable frequency and voltage v =v_(m) sin omega t, draw a plot showing the variation of current (I) with angular frequency (omega) for two different values of resistance R_(1) and R_(2) (R_(1) gt R_(2)) . Write the condition under which the phenomenon of resonance occurs. For which value of the resistance out of the two curves, a sharper resonance is produced ? Define Q-factor of the circuit and give its significance.
In the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t = 0 . Find the current I as a function of time if R=sqrt(L//C)
NCERT EXEMPLAR ENGLISH-ALTERNATING CURRENT-Long Answe types Questions
- An electrical device draws 2 kW power form AC mains [voltage 223 V (rm...
Text Solution
|
- 1 MW power is to be delivered from a power station to a town 10 km awa...
Text Solution
|
- Consider the L-C-R circuit shown in the fiure. Find the net current I ...
Text Solution
|
- For an LCR circuit driven at frequency omega, the equation reads L (di...
Text Solution
|
- In the LCR circuit shown in Fig., the ac driving voltage is upsilon = ...
Text Solution
|