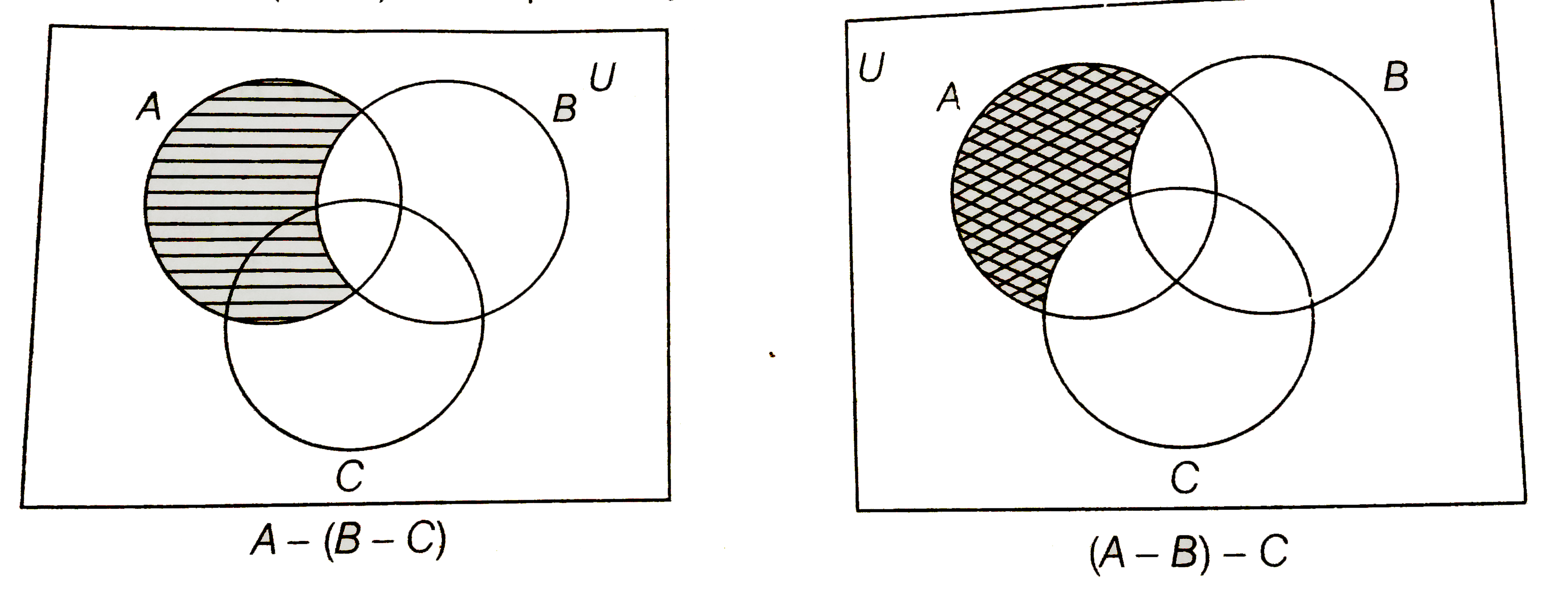Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-SETS-TRUE AND FALSE
- For all sets A, B and C, A - (B - C) = (A - B) - C.
Text Solution
|
- IF A any set, then A sub A.
Text Solution
|
- If M = { 1,2,3,4,5.6,7,8,9} and B = { 1,2,3,4,5.6,7,8,9}, then B canc...
Text Solution
|
- The sets {1,2,3,4} and {3,4,5,6} are equal
Text Solution
|
- Q uu Z = Q, where Q is the set of rational numbers and Z is the ...
Text Solution
|
- Let sets R and T be defined as R = {x in Z|x is divisible by 2} ...
Text Solution
|
- Given A = [0,,2], B = [x in R| 0 le x le 2}. Then, A = B.
Text Solution
|