Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-QUADRILATERALS -LONG ANSWER TYPE QUESTIONS
- A square is incribed in an isoceles right triangle, so that the square...
Text Solution
|
- In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ang...
Text Solution
|
- P, Q , R and S are respectively the mid-points of the sides AB, BC, C...
Text Solution
|
- ABCD is a rhombus and P, Q, R and S are wthe mid-points of the side...
Text Solution
|
- P, Q, R and S are respectively the mid-points of sides AB, BC, CD and ...
Text Solution
|
- If diagonal of a parallelogram bisects one of the angles of the para...
Text Solution
|
- ABCD is a parallelogram in which P and Q are mid-points of opposite ...
Text Solution
|
- ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that angleA...
Text Solution
|
- In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=E...
Text Solution
|
- In A B C ,A D is the median through A and E is the mid-point of A D ....
Text Solution
|
- Show that the quadrilateral, formed by joining the mid-points of the ...
Text Solution
|
- In Figure, A B C D isa trapezium in which side A B is a parallel to si...
Text Solution
|
- Prove that the quadrilateral formed by the bisectors of the angles of ...
Text Solution
|
- P and Q are points on opposite sides AD and BC of a parallelogram ABCD...
Text Solution
|
- ABCD is a rectangle in which diagonal BD bisects angle B. Show that AB...
Text Solution
|
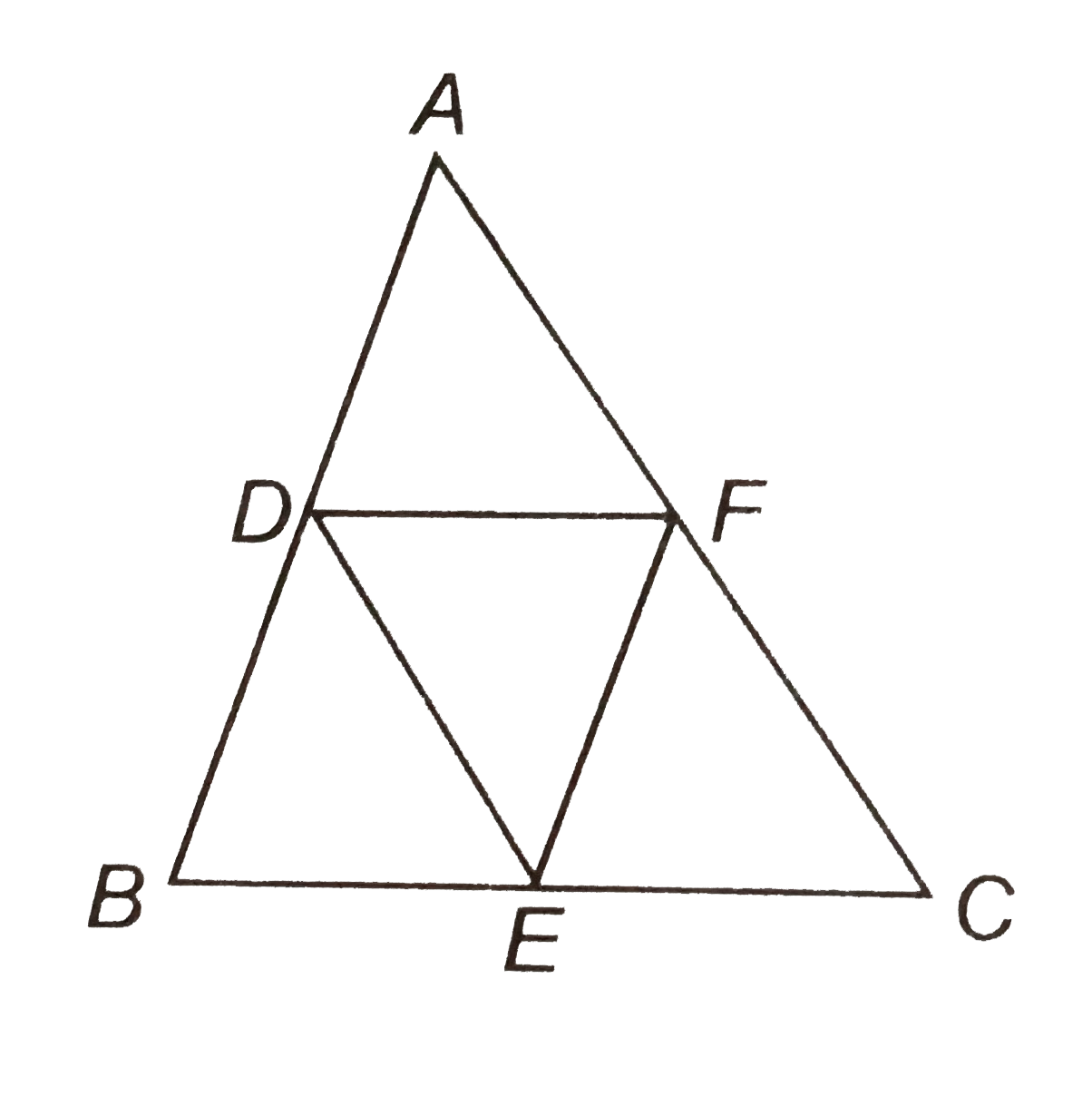
- In DeltaA B C, D, E and F are respectively the mid-points of sides AB...
Text Solution
|
- Prove that the line segment joining the mid-points of the diagonals of...
Text Solution
|
- P is the mid-point of the side CD of a parallelogram ABCD. A line thro...
Text Solution
|