Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-Areas of Parallelograms and Triangles-Exercise-9.4 Long Answer Type Questions
- A point E is taken on the side BC of a parallelogram ABCD. AE and DC a...
Text Solution
|
- The diagonals of a parallelogram ABCD intersect at a point O. Through ...
Text Solution
|
- The median BE and CF of a triangle ABC intersect at G. Prove that the ...
Text Solution
|
- In figure, CD || AE and CY || BA. Prove that ar (DeltaCBX) = ar (Delta...
Text Solution
|
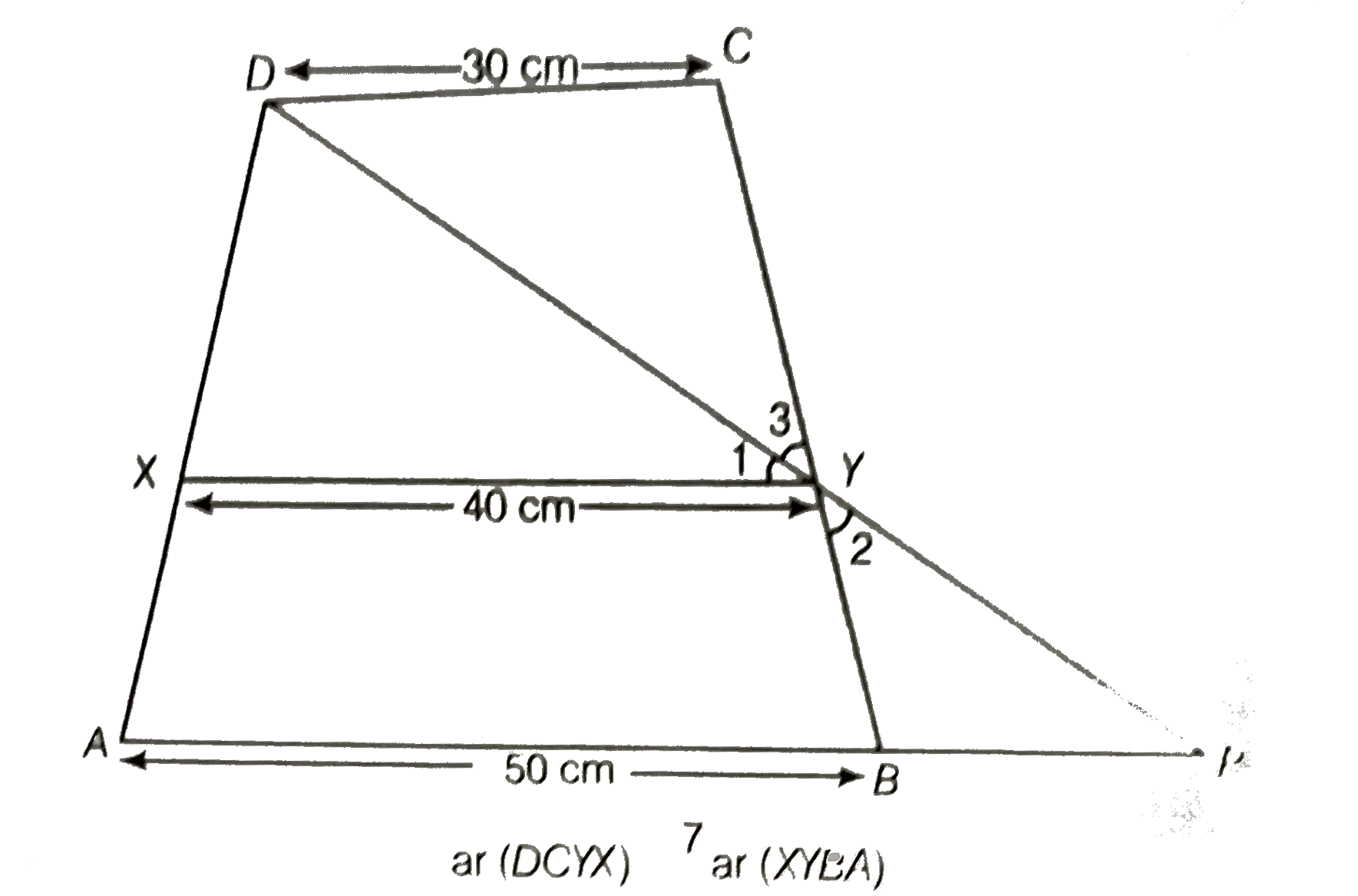
- ABCD is trapezium in which AB||DC, DC = 30 cm and AB = 50 cm. If X and...
Text Solution
|
- In DeltaABC , if L and M are the points on AB and AC, respectively suc...
Text Solution
|
- In figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC pro...
Text Solution
|
- If the medians of a triangleABC intersect at G, show that ar(triangl...
Text Solution
|
- In figure X and Y are the mid-points of AC and AB respectively, QP || ...
Text Solution
|
- In figure, ABCD and AEFD are two parallelograms. Prove that ar (DeltaP...
Text Solution
|