Home
Class 9
MATHS
The sides of a triangle are 35 cm, 54 cm...

The sides of a triangle are `35` `cm`, `54` `cm` and `61` `cm`, respectively. The length of its longest altitude

A

`16sqrt5` cm

B

`10sqrt5` cm

C

`24sqrt5` cm

D

28 cm

Text Solution

Verified by Experts

The correct Answer is:
C
(c) Let ABC be a triangle in which sides AB=35 cm, BC=54 cm and CA=61 cm

Now, semi-perimeter of a triangle,
`s=(a+b+c)/(2)=(35+54+61)/(2)=(150)/(2)=75 cm`
`[because"semi-perimeter",s=(a+b+c)/(2)]`
`because"Area of" triangleABC=sqrt(s(s-a)(s-b)(s-c))`
`=sqrt(75(75-35)(75-54)(75-61))`
`=sqrt(75xx40xx21xx14)`
`=sqrt(25xx3xx4xx2xx5xx7xx3xx7xx2)`
`=5xx2xx2xx3xx7sqrt5=240sqrt5cm^(2)`
`"Also", " Area of"triangleABC=(1)/(2)xxABxx"Altitude"`
`rArr (1)/(2)xx35xxCD=420sqrt5`
`rArr CD=(420xx2sqrt5)/(35)`
`therefore CD=24sqrt5`
Hence, the length of altitude is `24sqrt5 cm.`
Promotional Banner

Topper's Solved these Questions

  • HERON'S FORMULA

    NCERT EXEMPLAR ENGLISH|Exercise Very Short Answer Type Questions|9 Videos

  • HERON'S FORMULA

    NCERT EXEMPLAR ENGLISH|Exercise Short Answer Type Questions|10 Videos

  • COORDINATE GEOMETRY

    NCERT EXEMPLAR ENGLISH|Exercise Exercise 3.4 Long Answer Type Questions|5 Videos

  • INTRODUCTION TO EUCLID GEOMETRY

    NCERT EXEMPLAR ENGLISH|Exercise Exercise 5.4 Long Answer Type Questions|5 Videos

Similar Questions

Explore conceptually related problems

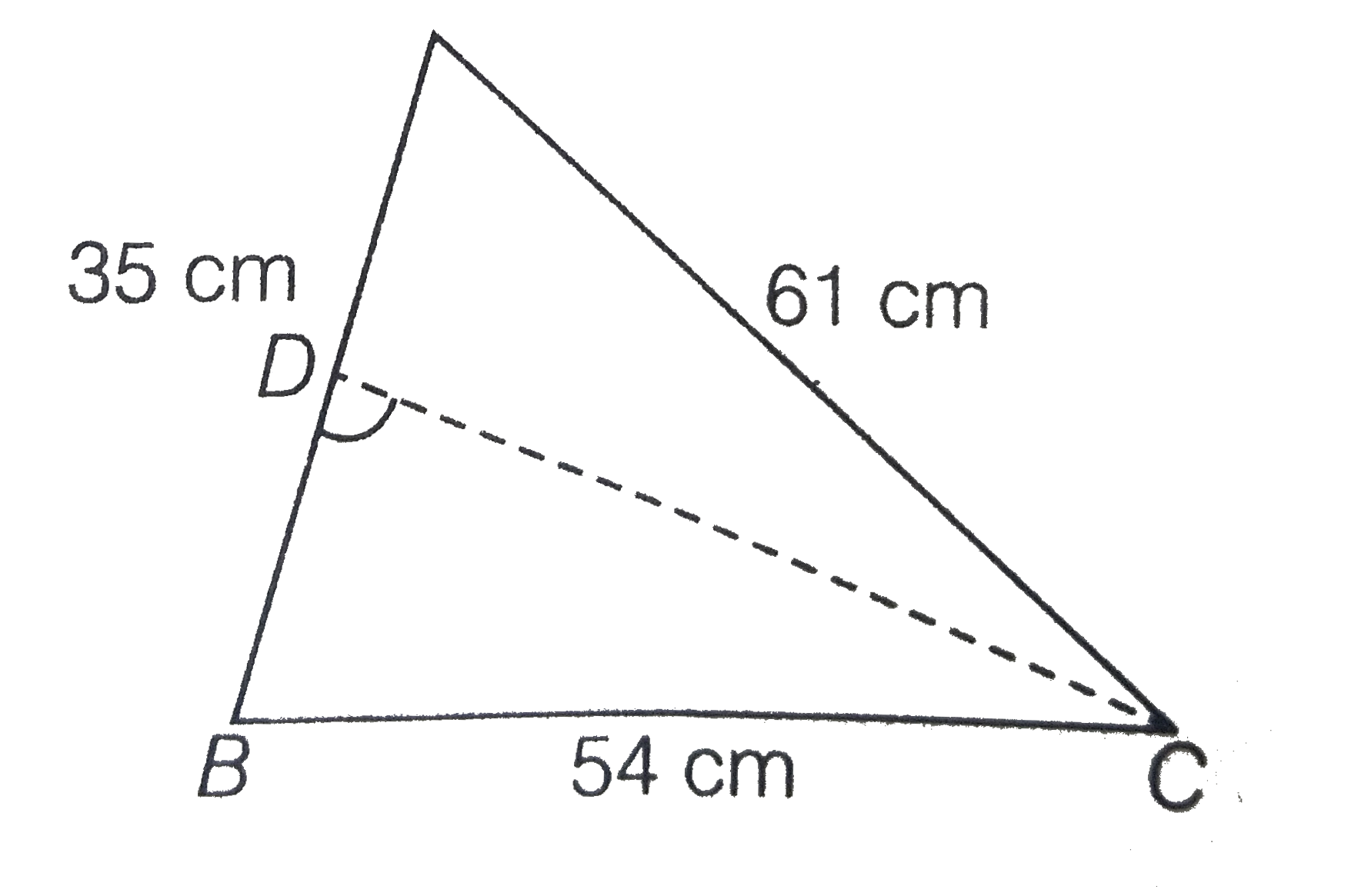
The sides of a triangle are 5 cm, 8 cm and 11 cm respectively. Demtermine whether it is a right angled triangle or not.

Find the area of a triangle whose sides are 3cm, 4cm and 5cm respectively.

A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.

A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.

The areas of two similar triangles are 169\ c m^2 and 121\ c m^2 respectively. If the longest side of the larger triangle is 26cm, what is the length of the longest side of the smaller triangle?

Two sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.

If two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be

The areas of two similar triangles are 169\ c m^2 and 121\ c m^2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.

Find the area of triangle whose sides are 5 cm, 12 cm and 13 cm. Also, find the length of its altitude corresponding to the longest side.

Find the area of triangle whose sides are 17 cm, 8 cm and 15 cm. Also calculate the length of the altitude corresponding to the largest side of the triangle.