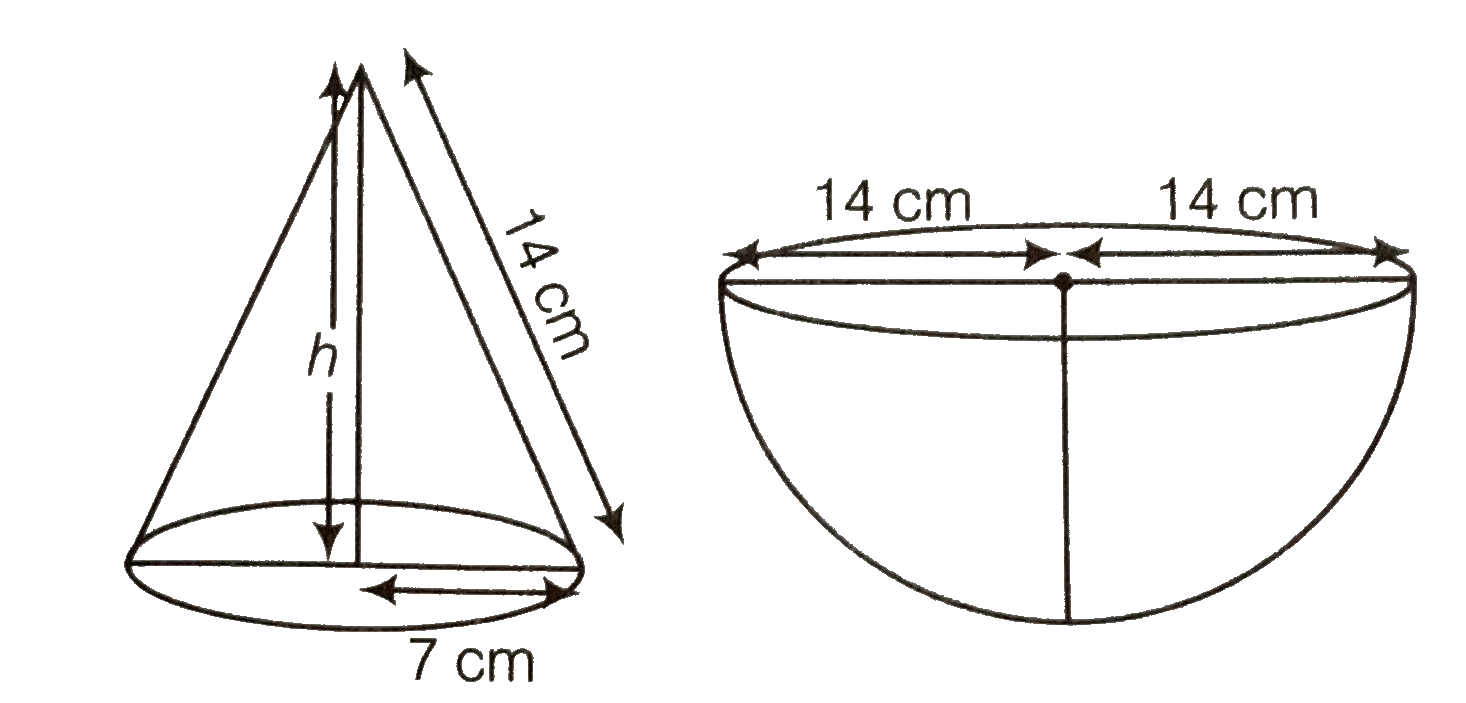
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-VOLUME AND SURFACE AREA-LONG ANSWER TYPE QUESTIONS
- A cylindical tube opened at both the ends is made of iron sheet ...
Text Solution
|
- A semi-circular sheet of metal of diameter 28cm is bent into an ope...
Text Solution
|
- A cloth having an area of 165 m^(2) is shaped into the form of a coni...
Text Solution
|
- The water for a factory is stored in a hemispherical tank whose inte...
Text Solution
|
- If volumes of two spheres are in the ratio 64:27 then the ratio of the...
Text Solution
|
- A cube of side 4 cm contains a sphere touching its side. Find the vo...
Text Solution
|
- A sphere and a right circular cylinder of the same radius have equal ...
Text Solution
|
- 30 circular plants, each of radius 14 cm and thickness 3 cm are place...
Text Solution
|