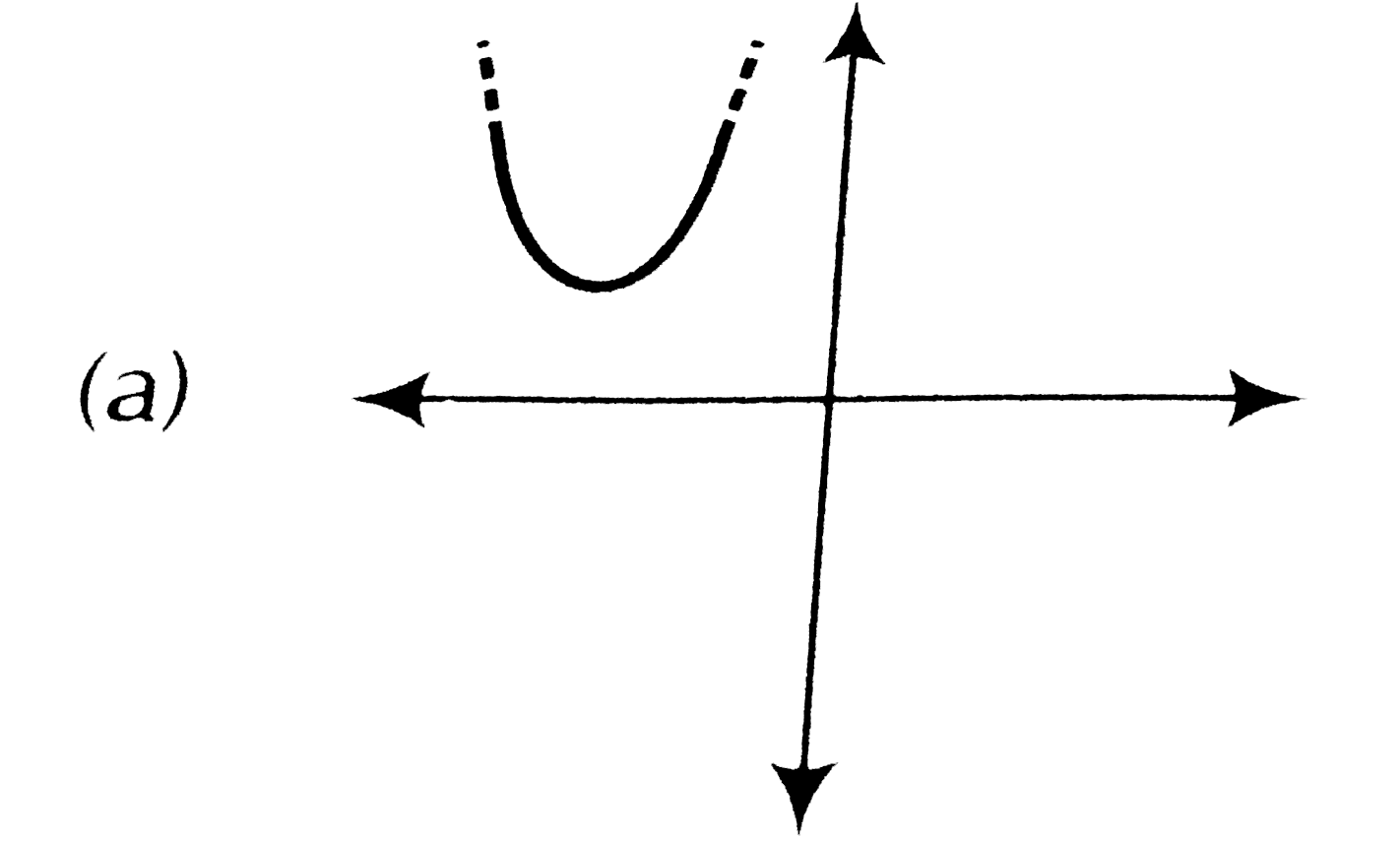
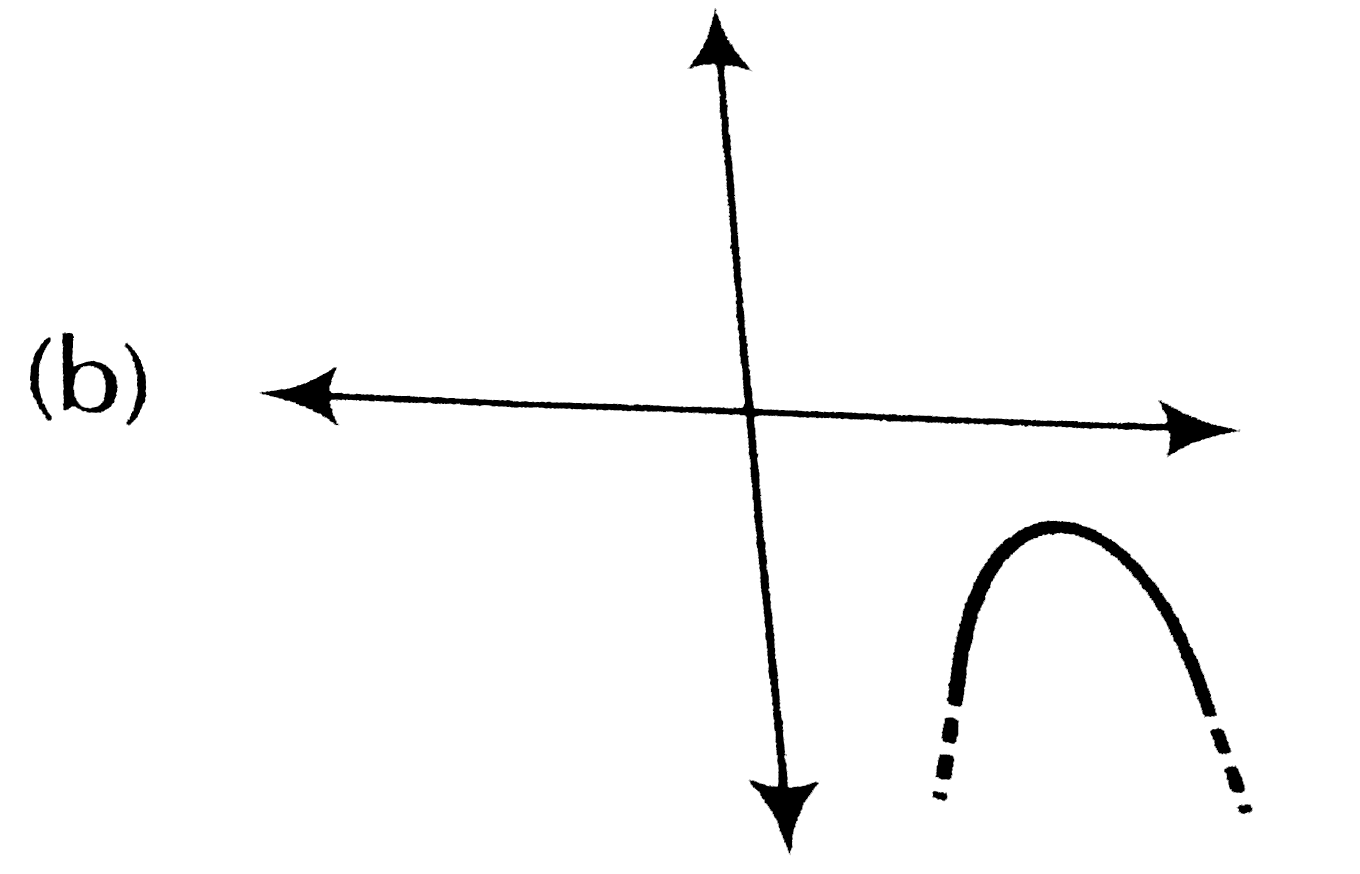
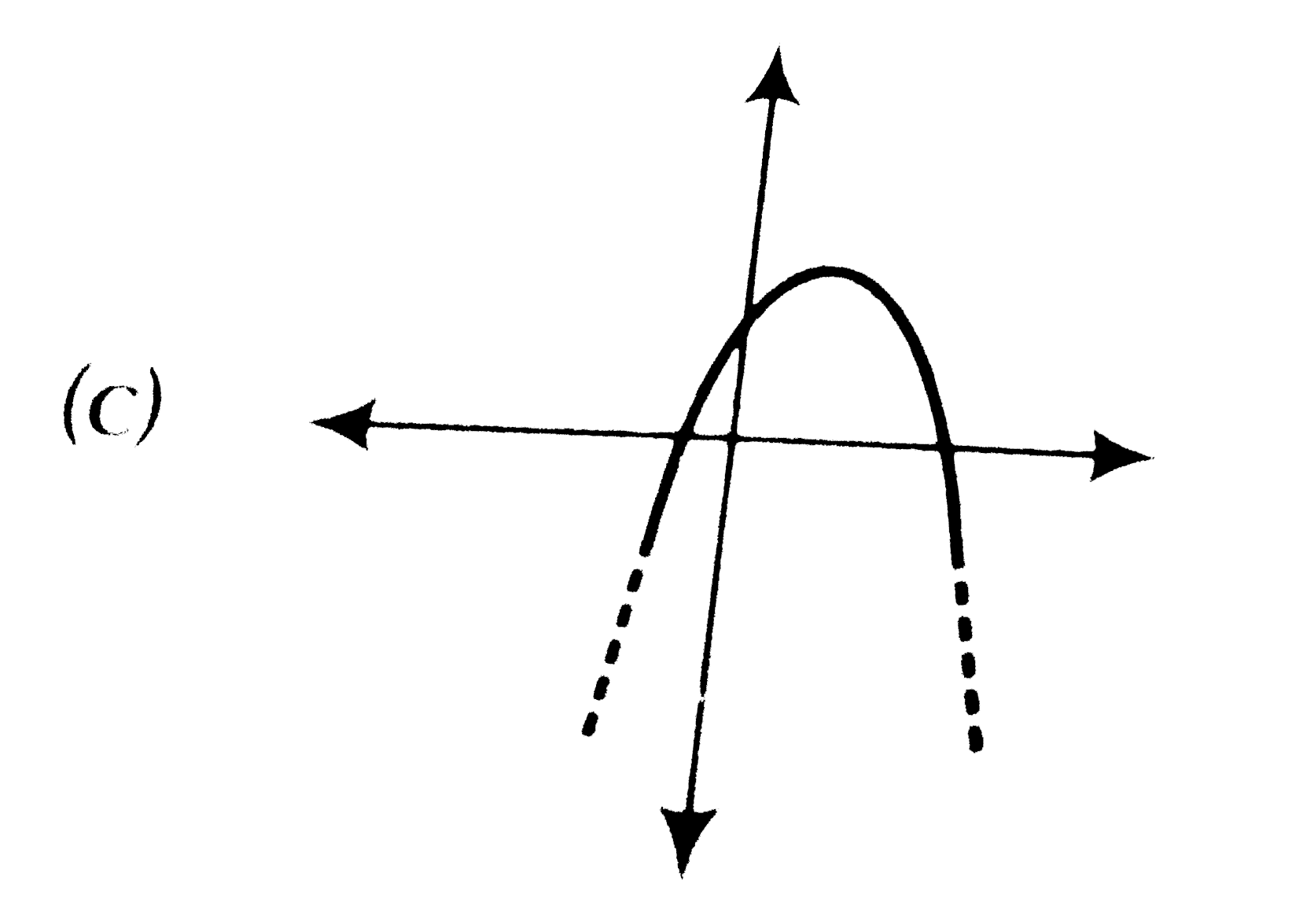
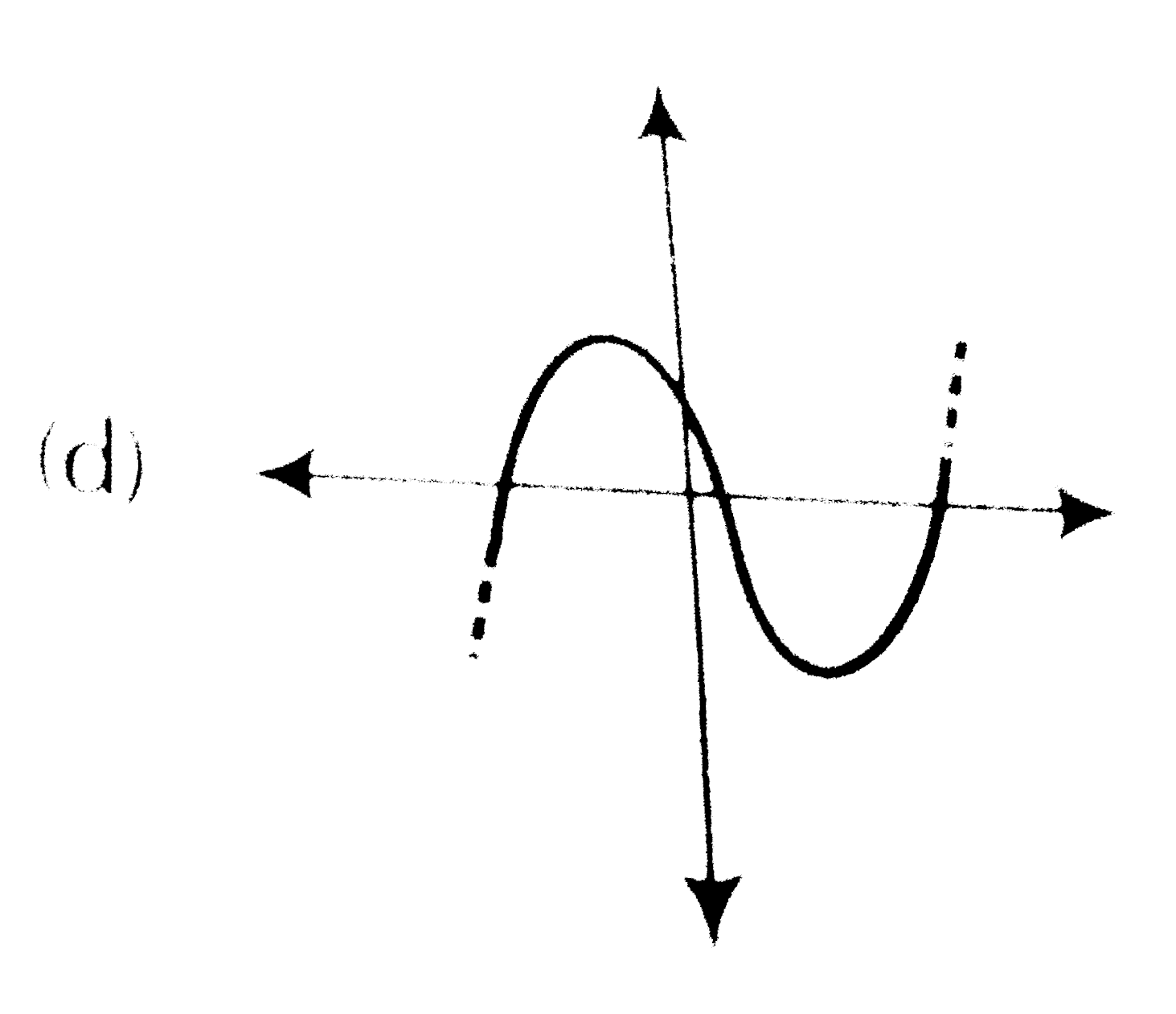
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
POLYNOMIALS
NCERT EXEMPLAR ENGLISH|Exercise Very Short Answer Type Questions|2 VideosPOLYNOMIALS
NCERT EXEMPLAR ENGLISH|Exercise Short Answer Type Questions|10 VideosPAIR OF LINEAR EQUATIONS IN TWO VARIABLES
NCERT EXEMPLAR ENGLISH|Exercise Exercise 3.4 Long Answer Type Questions|13 VideosQUADRIATIC EQUATIONS
NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPE|12 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-POLYNOMIALS -Long Answer Type Questions
- Which of the following is not the graph of a quadratic polynomial?
Text Solution
|
- For each of the following find a quadratic polynomial whose sum and pr...
Text Solution
|
- Given that zeroes of cubic polynomial x^(3)-6x^(2)+3x+10 are of the fo...
Text Solution
|
- If sqrt2 is a zero of p(x)=6x^3 +sqrt2x^2- 10x -4sqrt2 , find the rema...
Text Solution
|
- The value of k, if x^2+2x+k is a factor of 2x^4+x^3-14x^2+5x+6 is
Text Solution
|
- If x - sqrt(5) is a factor of the cubic polynomial x^(3)-3sqrt(5)x^(2)...
Text Solution
|
- For which values of a and b, the zeroes of q(x) = x^(3)+2x^(2)+a are a...
Text Solution
|