Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-TRIANGLES-Short Answer Type Questions
- In P Q R ,\ \ Q M|P R and P R^2-P Q^2=Q R^2 . Prove that Q M^2=P M...
Text Solution
|
- Find the value of x for which DEabs()AB in given figure.
Text Solution
|
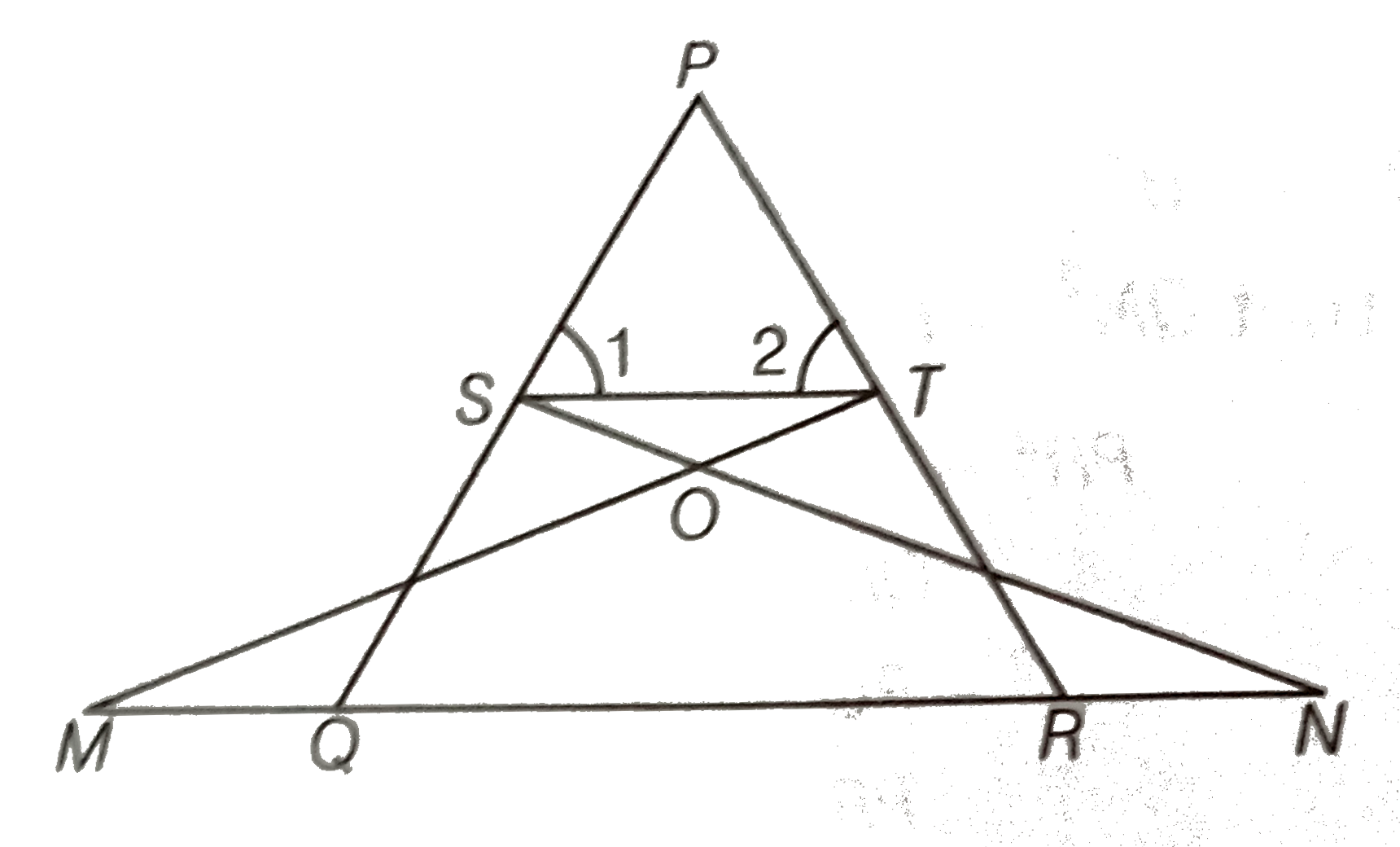
- In figure, if angle1=angle2 and DeltaNSQ=DeltaMTR, then prove that Del...
Text Solution
|
- Diagonals of a trapezium PQRS intersect each other at the point 0 ,PQa...
Text Solution
|
- In figure , if Ababs()DC and AC, PQ interrest each other at the point ...
Text Solution
|
- Find the altitude of an equilateral triangle of side 8 cm.
Text Solution
|
- If DeltaABC~DeltaDEF, AB=4cm, DE=6, EF=9 cm and FD=12 cm, then find th...
Text Solution
|
- In figure, if DEabs()BC, then find the ratio of ar (DeltaADE) and ar(D...
Text Solution
|
- ABCD is a trapezium in which ABabs()DC and P,Q are points on AD and BC...
Text Solution
|
- Corresponding sides of two triangles are in the ratio 2\ :3 . If th...
Text Solution
|
- In a Delta PQR, N is a point on PR, such that QNbotPR. If PNcdotNR=QN^...
Text Solution
|
- The areas of two similar triangles are 36\ c m^2 and 100\ c m^2 . I...
Text Solution
|
- In given figure, if angleACB=angleCDA,AC=8cm and AD=3 cm, then find BD...
Text Solution
|
- A 15 high tower casts a sshadow 24 long at a certain time at the same ...
Text Solution
|
- Foot of a 10 m long ladder leaning against a verticle wall is 6 m away...
Text Solution
|