Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-CIRCLES-EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
- If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF=BC+...
Text Solution
|
- Let s denotes the semi-perimeter of a DeltaABC in which BC=a, CA=b and...
Text Solution
|
- From an external point P, two tangents, PA and PB are drawn to a circl...
Text Solution
|
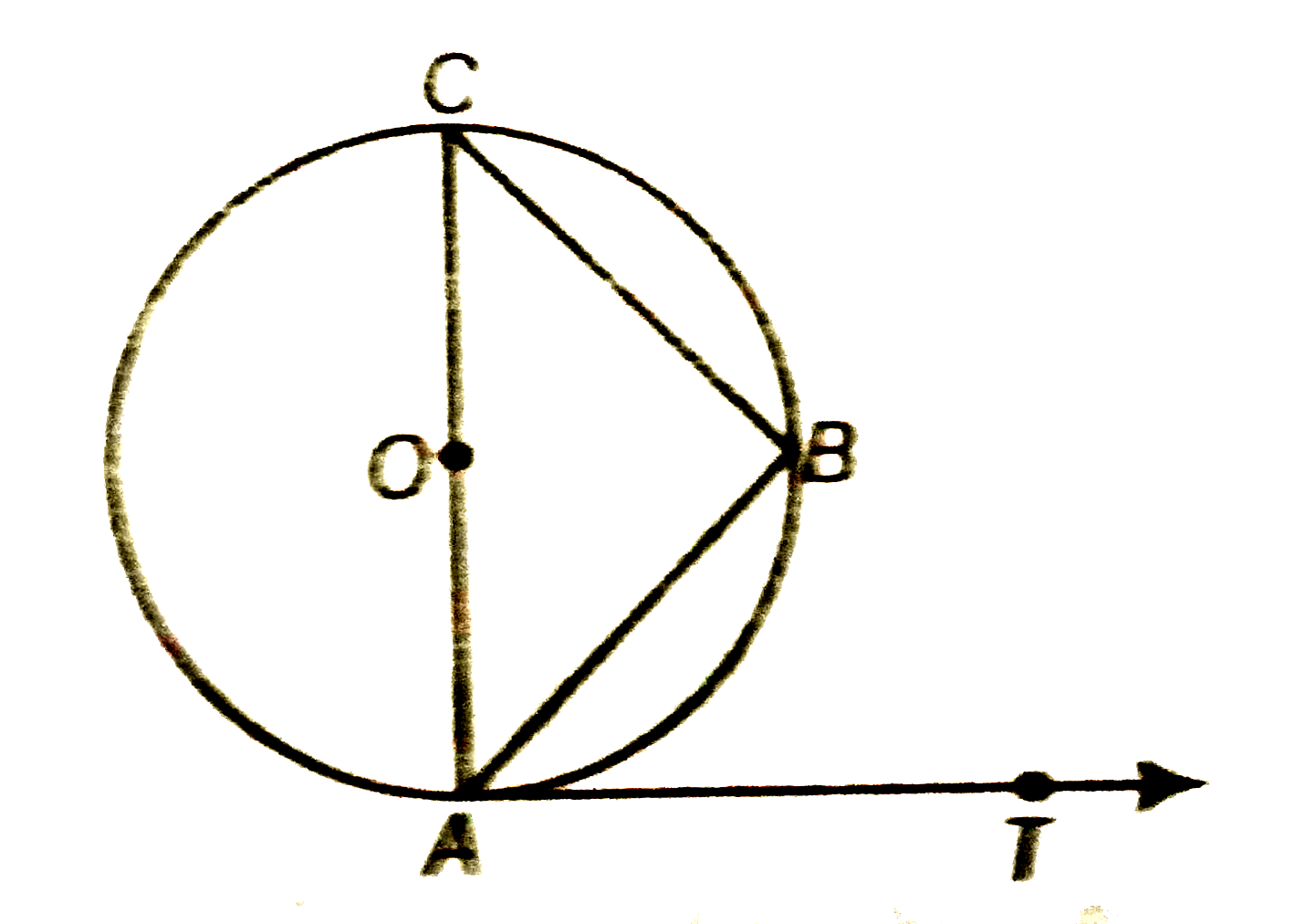
- If AB is chord of a circle with centre O, AOC is a diameter and AT is ...
Text Solution
|
- Two circles with centers O and O' of radii 6cm and 8 cm respectively i...
Text Solution
|
- In a right angle triangle Delta ABC is which / B = 90^@ a circle is dr...
Text Solution
|
- In figure, tangents PQ and PR are drawn to a circle such that angleRPQ...
Text Solution
|
- AB is a diameter of a circle and AC is its chord such that angleBAC=30...
Text Solution
|
- . Prove that the tangent drawn at the mid-point of an arc of a circle ...
Text Solution
|
- In a figure the common tangents, AB and CD to two circles with centers...
Text Solution
|
- Type V: O is the center of the circle of radius 5cm. T is a point such...
Text Solution
|
- The tangent at a point C of a circle and a diameter AB when extended i...
Text Solution
|
- If an isosceles triangle A B C in which A B=A C=6c m is inscribed in a...
Text Solution
|
- A is a point at a distance 13 cm from the centre O of a circle of radi...
Text Solution
|