Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
NCERT EXEMPLAR ENGLISH|Exercise TRUE/FALSE|9 VideosSTRAIGHT LINES
NCERT EXEMPLAR ENGLISH|Exercise MATCHING THE COLUMN|3 VideosSTRAIGHT LINES
NCERT EXEMPLAR ENGLISH|Exercise Objective type questions|20 VideosSTATISTICS
NCERT EXEMPLAR ENGLISH|Exercise FILLERS|7 VideosTRIGONOMETRIC FUNCTIONS
NCERT EXEMPLAR ENGLISH|Exercise TRUE/FALSE|9 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-STRAIGHT LINES-Fillers
- If a , b and c are in A P , then the straight line a x+b y+c=0 will...
Text Solution
|
- Find the equation of the straight line which passes through the point ...
Text Solution
|
- Find the equation of the lines through the point (3, 2) which make an...
Text Solution
|
- The points (3,4) and (2,-6) are situated on the .......... Of the line...
Text Solution
|
- A point moves so that square of its distance from the point (3,-2) is ...
Text Solution
|
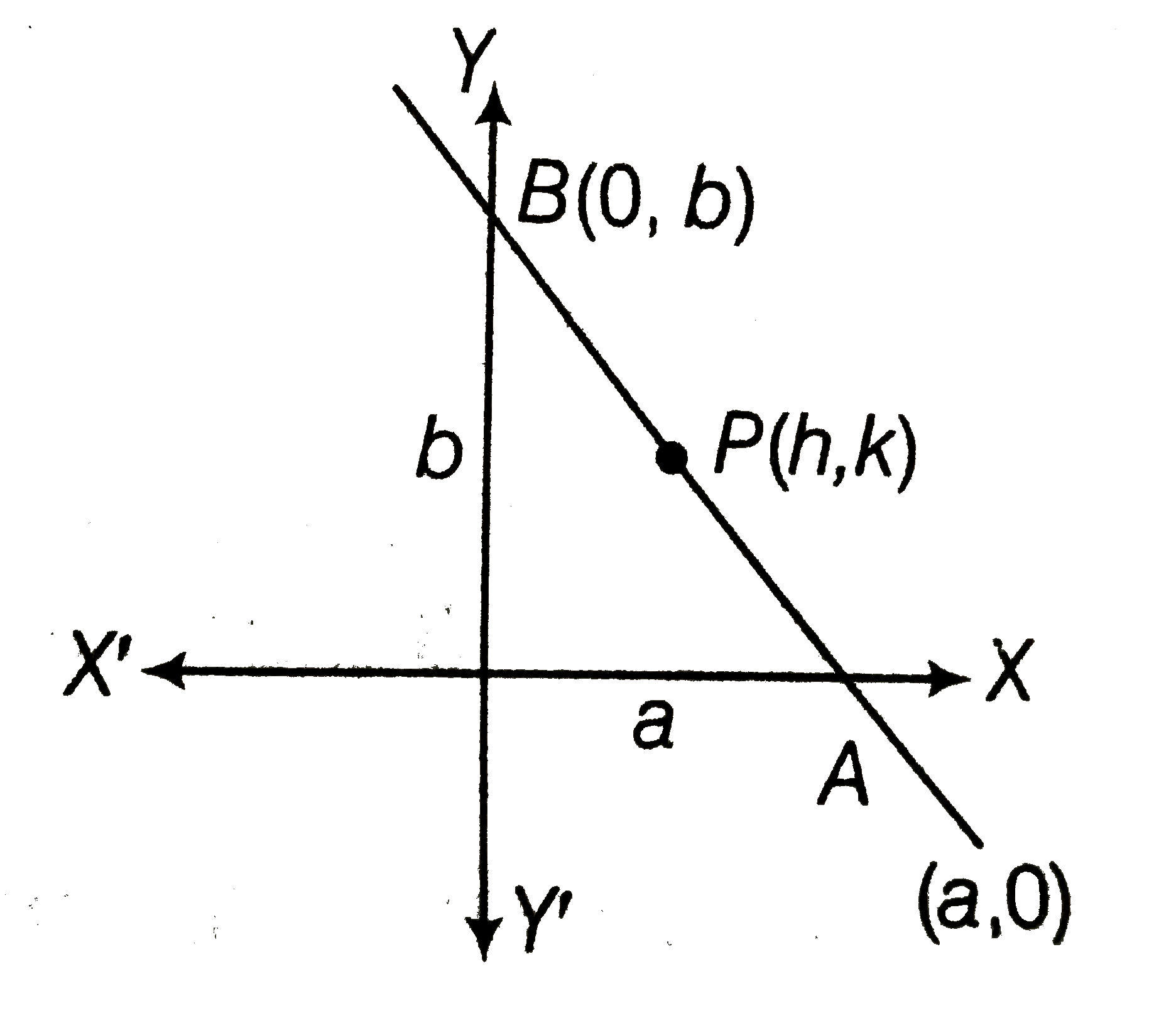
- Find the locus of the mid-point of the portion of the line xcosalpha+y...
Text Solution
|