From the shaded region, it is clear that feasible region is unbouded with the corner points A (4,0), B(2,1), and C(0,3)
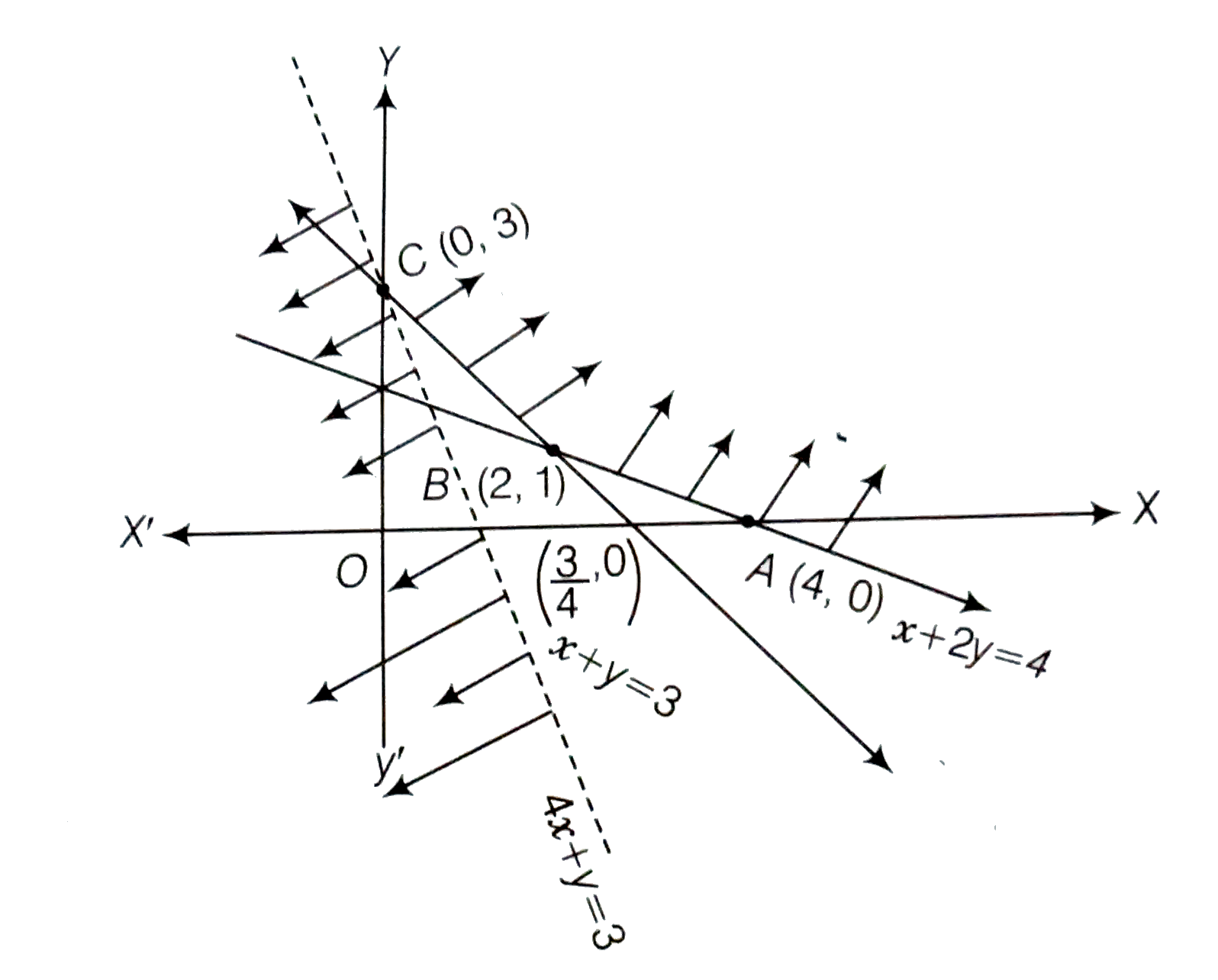
Now we see that 3 is the smallest value of Z at the corner point (0,3). Note that here we see that the region is unbounded, therefore 3 may or may not be the minimum value of Z. To decided this issue, we graph the inequality `4x+ y le 3` and check whether ther resulting open half plan has not point in common with feasible reigon otherwise, Z has no minimum value. From the shown graph above,it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0,3)