Home
Class 12
MATHS
The feasible region for an LPP is shown ...

The feasible region for an LPP is shown in the following figure. Let `F=3x--4y` be the objective function. Maximum value of F is

A

0

B

8

C

12

D

`-18`

Text Solution

Verified by Experts

The correct Answer is:
C
The feasible region as shown in the region has objective funciton F=3x-4y.

Hence, the maximum value of F is 12.
Promotional Banner

Topper's Solved these Questions

  • LINEAR PROGRAMMING

    NCERT EXEMPLAR ENGLISH|Exercise FILLERS|7 Videos

  • LINEAR PROGRAMMING

    NCERT EXEMPLAR ENGLISH|Exercise TRUE/FALSE|2 Videos

  • LINEAR PROGRAMMING

    NCERT EXEMPLAR ENGLISH|Exercise TRUE/FALSE|2 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    NCERT EXEMPLAR ENGLISH|Exercise Fillers|18 Videos

  • MATRICES

    NCERT EXEMPLAR ENGLISH|Exercise Solved example|101 Videos

Similar Questions

Explore conceptually related problems

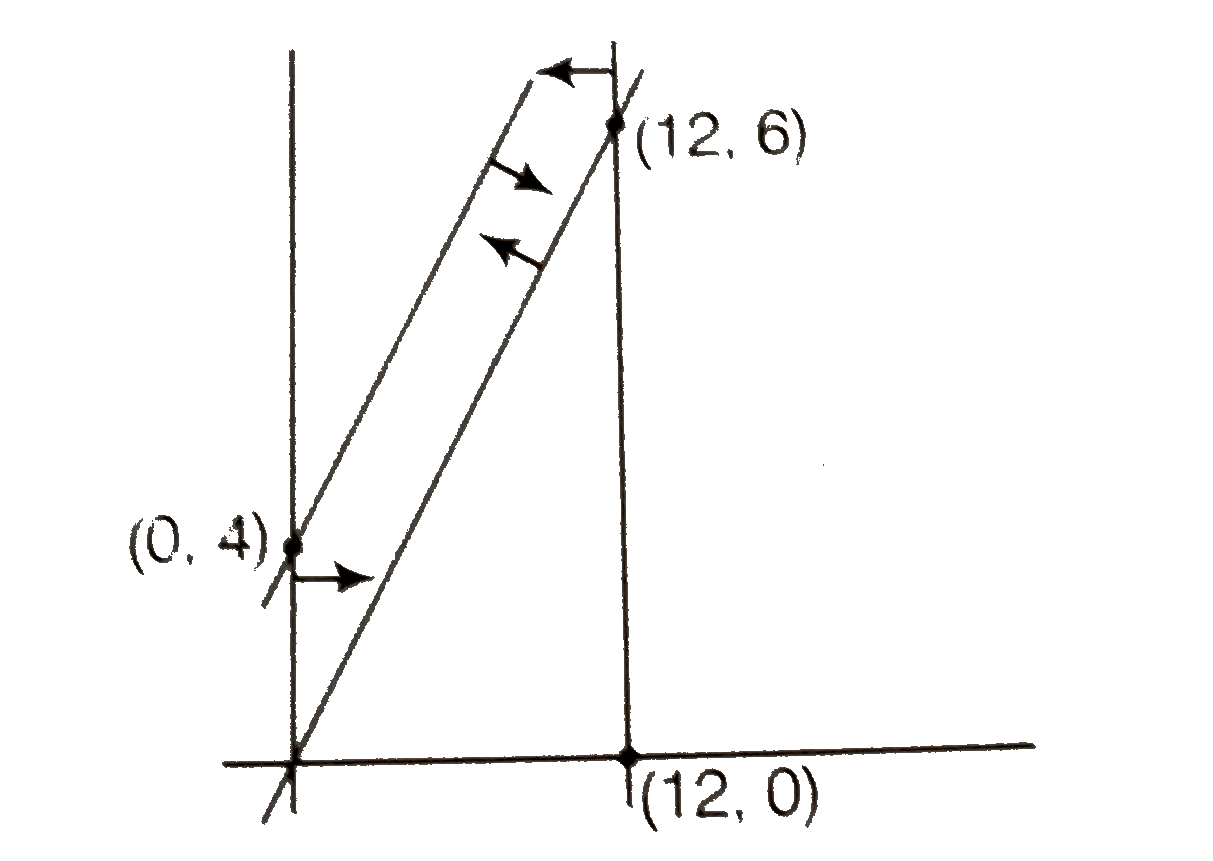
The feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at

The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

Feasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

The feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

Corner points of the feasible region for an LPP are ( 0,2) (3,0) ,(6,0),(6,8) and (0,5) Let Z=4 x + 6y be the objective function. The minimum value of F occurs at?

In the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.

Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F-4x+6y be the objective function. Determine the minimum valur of F occurs at

If the feasibile region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.

The graph of y=f(x) is as shown in the following figure. Draw the graph of y=[f(x)] .

In the given graph,the feasible region for a LPP is shaded. The objective function Z=2x-3y ,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)