Text Solution
Verified by Experts
Topper's Solved these Questions
LAWS OF MOTION
NCERT EXEMPLAR ENGLISH|Exercise Long answer Type Questions|9 VideosLAWS OF MOTION
NCERT EXEMPLAR ENGLISH|Exercise Very short answer type Questions|12 VideosKINETIC THEORY
NCERT EXEMPLAR ENGLISH|Exercise Multiple Choice Questions (MCQs)|31 VideosMECHANICAL PROPERTIES OF FLUIDS
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|3 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-LAWS OF MOTION-Short answer type questions
- Two masses of 5kg and 3kg are suspended with help of massless inextens...
Text Solution
|
- Block A of weight 100N rests on a frictionless inclined plane of slope...
Text Solution
|
- A block of mass M is held against a rough vertical wall by pressing it...
Text Solution
|
- a 100kg gun fires a ball of 1kg horizontally from a cliff of height 50...
Text Solution
|
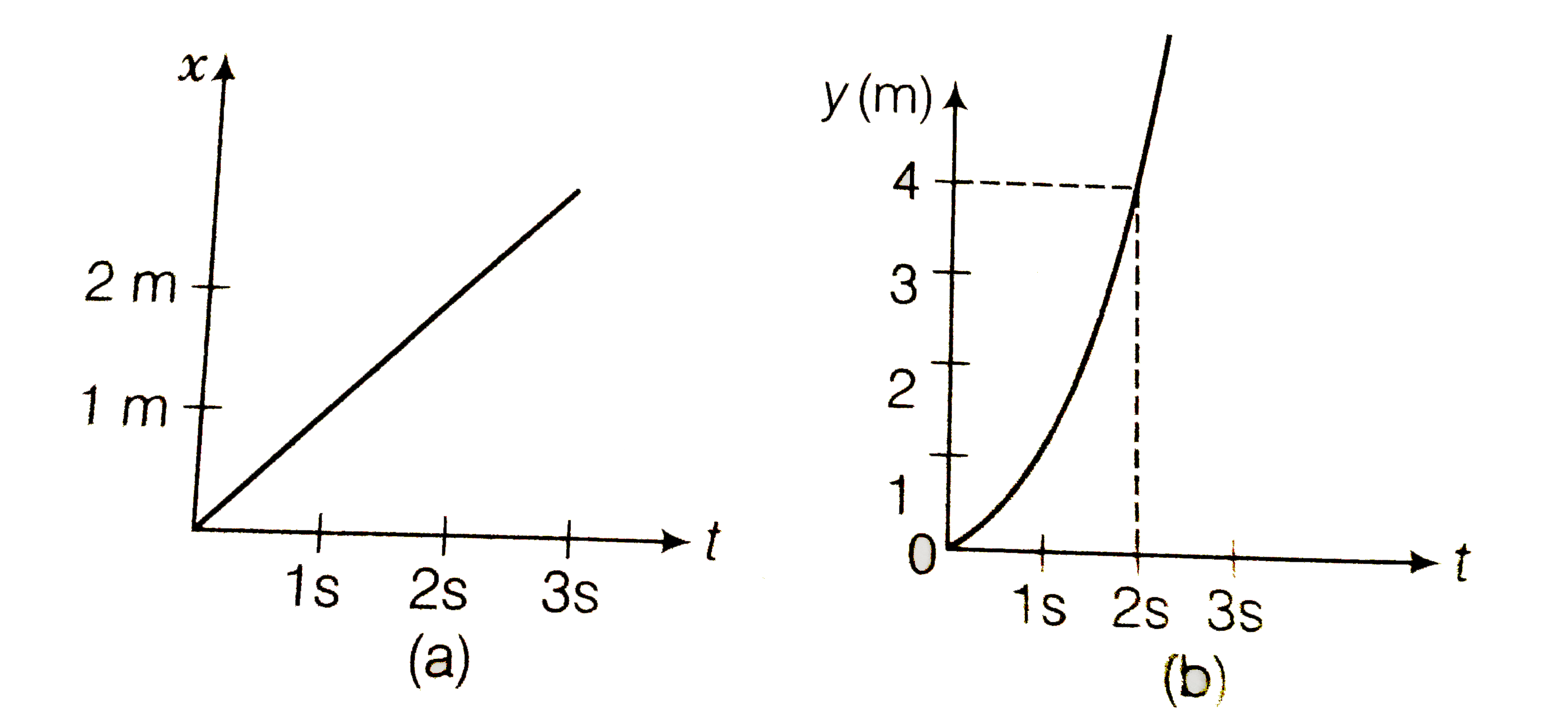
- Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions...
Text Solution
|
- A person in an elevator accelerating upwards with an acceleration of ...
Text Solution
|