Text Solution
Verified by Experts
Topper's Solved these Questions
SURFACE AREAS AND VOLUMES
NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPE QUESTIONS|20 VideosSURFACE AREAS AND VOLUMES
NCERT EXEMPLAR ENGLISH|Exercise VERY SHORT ANSWER TYPE QUESTIONS|8 VideosSTATISTICS AND PROBABILITY
NCERT EXEMPLAR ENGLISH|Exercise LONG ASWERS QUESTIONS|14 VideosTRIANGLES
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|18 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-SURFACE AREAS AND VOLUMES-SHORT ANSWER TYOE QUESTIONS
- Three metallic solid cubes whose edges are 3 cm ,4 cm and 5 cm melted...
Text Solution
|
- How many shots each having diameter 3 cm can be made form a cuboid...
Text Solution
|
- A bucket is in the form of a frustum of a cone and holds 28.490 lit...
Text Solution
|
- A cone of radius 8 cm and height 12 cm is divided into two parts by a ...
Text Solution
|
- 2 cubes each of volume 64"\ "c m^3 are joined end to end. Find the ...
Text Solution
|
- From a solid cube of side 7 cm, a conical cavity of height 7 cm and ...
Text Solution
|
- Two cones with same base radius 8 cm and height 15 cm are joine...
Text Solution
|
- Two solid cones A and B are placed in a cylindrical tube as shown in t...
Text Solution
|
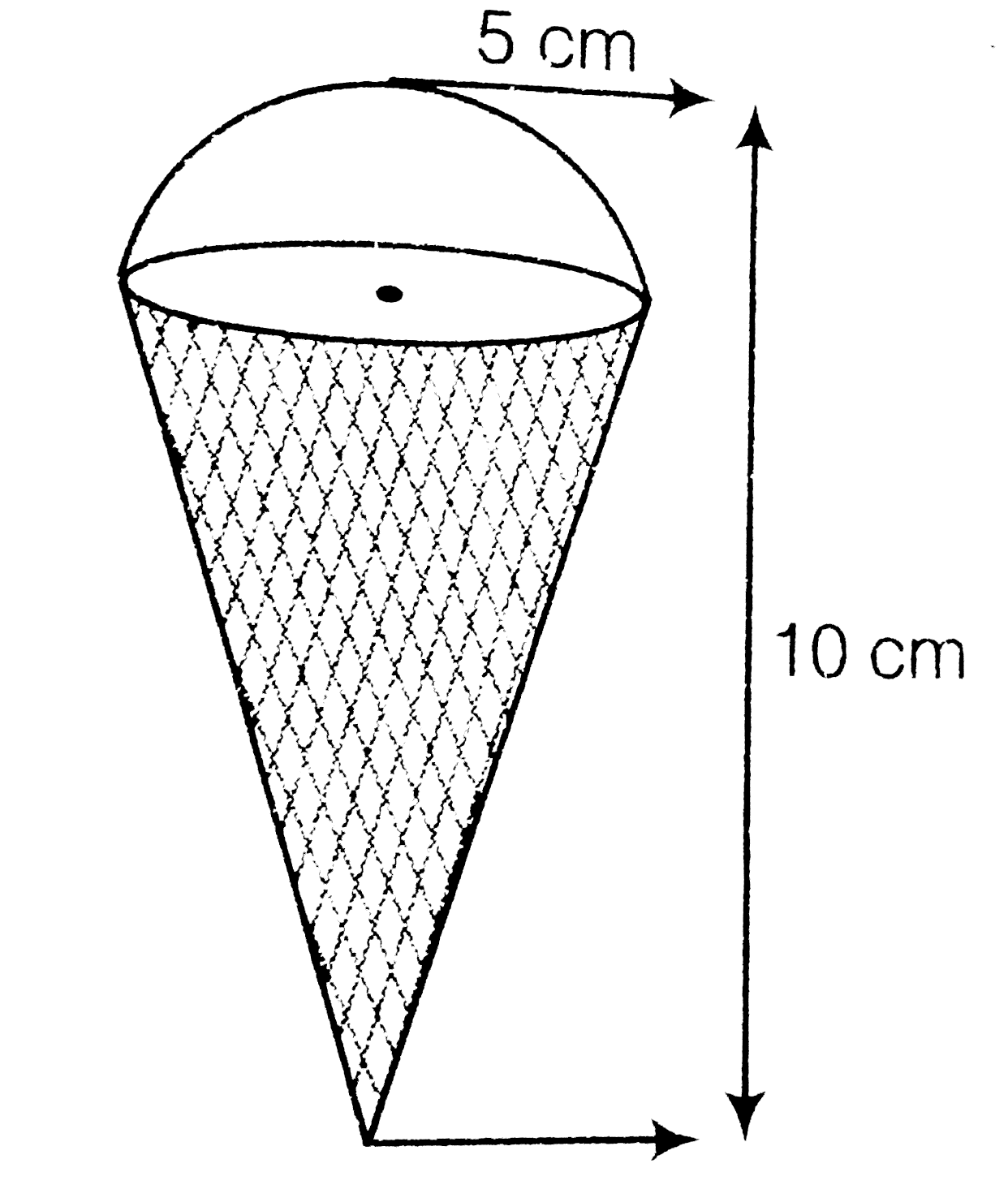
- An ice-ceram cone full of ice-cream having radius 5 cm height 10 c...
Text Solution
|
- Mearbles of diameter 1.4 cm are dropped into a cylindrical beaker of d...
Text Solution
|
- How many spherical lead shots each 4.2 cm in diameter can be obtain...
Text Solution
|
- How many spherical bullets can be made out of a solid cube of lead ...
Text Solution
|
- A wall 24 m long, 0.4 m thick and 6 m high is constructed with the br...
Text Solution
|
- Find the number of coins, 1.5 cm in diameter and 0.2 cm thick, to b...
Text Solution
|