Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATION OF INTEGRALS
NCERT EXEMPLAR ENGLISH|Exercise Objective Type Questions|22 VideosAPPLICATION OF INTEGRALS
NCERT EXEMPLAR ENGLISH|Exercise Objective Type Questions|22 VideosAPPLICATION OF DERIVATIVES
NCERT EXEMPLAR ENGLISH|Exercise Fillers|5 VideosCONTINUITY AND DIFFERENTIABILITY
NCERT EXEMPLAR ENGLISH|Exercise True/False|10 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Long Answer Type Questions
- Find the area of the region bounded by the curve y^(2)=2x" and "x^(2)+...
Text Solution
|
- Find the area of region by the curve y=sinx" between "x=0" and "x=2pi.
Text Solution
|
- Using integration, find the area of the region bounded by the triangle...
Text Solution
|
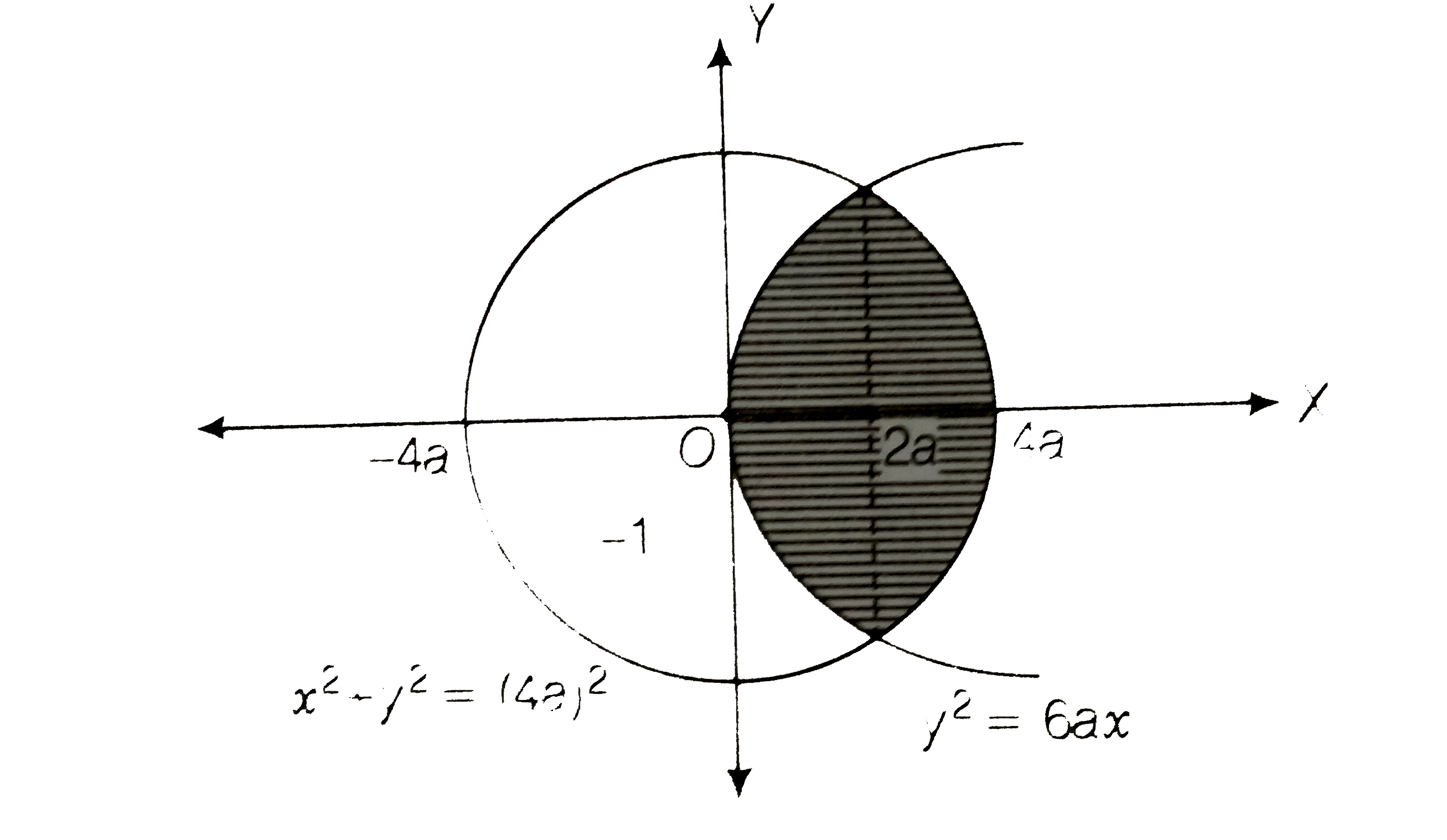
- Find the area of the region {(x, y) : y^2 =6ax and x^2+y^2=16a^2} us...
Text Solution
|
- Compute the area bounded by the lines x + 2y = 2 , y -x = 1 and 2x + y...
Text Solution
|
- Find the area bounded by the lines y=4x+5, y=5-x" and "4y=x+5.
Text Solution
|
- Find the area bounded by the curve y=2 cosx and the X-axis from x = ...
Text Solution
|
- Draw a rough sketch of the given curve y=1+abs(x+1),x=-3, x=3, y=0 and...
Text Solution
|
- Find the area of the region bounded by the curve y^(2)=2x" and "x^(2)+...
Text Solution
|
- Find the area of region by the curve y=sinx" between "x=0" and "x=2pi.
Text Solution
|
- Using integration find the area of region bounded by the triangle who...
Text Solution
|
- Find the area of the region {(x, y) : y^2 =6ax and x^2+y^2=16a^2} us...
Text Solution
|
- Compute the area bounded by the lines x + 2y = 2 , y -x = 1 and 2x + y...
Text Solution
|
- Find the area bounded by the lines y=4x+5, y=5-x" and "4y=x+5.
Text Solution
|
- Find the area bounded by the curve y=2 cosx and the X-axis from x = ...
Text Solution
|
- Draw a rough sketch of the given curve y=1+abs(x+1),x=-3, x=3, y=0 and...
Text Solution
|