Home
Class 10
MATHS
Find the area of the flower bed (with s...

Find the area of the flower bed (with semi-circular ends) shown in figure.

Text Solution

Verified by Experts

Length and breadth of a circular bed are 38 cm and 10 cm .
`:.` Area of rectangle ACDF = `"Length" xx"Breadth"= 38 xx 10= 380cm^(2)`
Both ends of flower bed are semi-circles.
`:.` Redius of semi-circle= `(DF)/(2)= (10)/(2)=5cm`
`:.` Area of one semi-circles = `(pir^(2))/(2)= (pi)/(2) (5)^(2)= (25pi)/(2) cm^(2)`
`:.` Area of two semi-circles= `2xx(25)/(2)pi = 25pi cm^(2)`
`:.` Total area of flower bed = Area of rectangle ACDF + Area of two semi-circles
= `(380+25pi) cm^(2)`
Promotional Banner

Topper's Solved these Questions

  • AREAS RELATED TO CIRCLE

    NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|20 Videos

  • AREAS RELATED TO CIRCLE

    NCERT EXEMPLAR ENGLISH|Exercise Very Short Answer Questions|14 Videos

  • ARITHMETIC PROGRESSIONS

    NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|10 Videos

Similar Questions

Explore conceptually related problems

Find i in shown figure.

Find the magnetic field at the centre of the circular loop shown in figure.

Find the area of the blades of the magnetic compass as shown in figure

The adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find: (i) the area of the whole land (ii) the area of the flower bed (iii) the area of the lawn excluding the area of the flower bed (iv) the circumference of the flower bed.

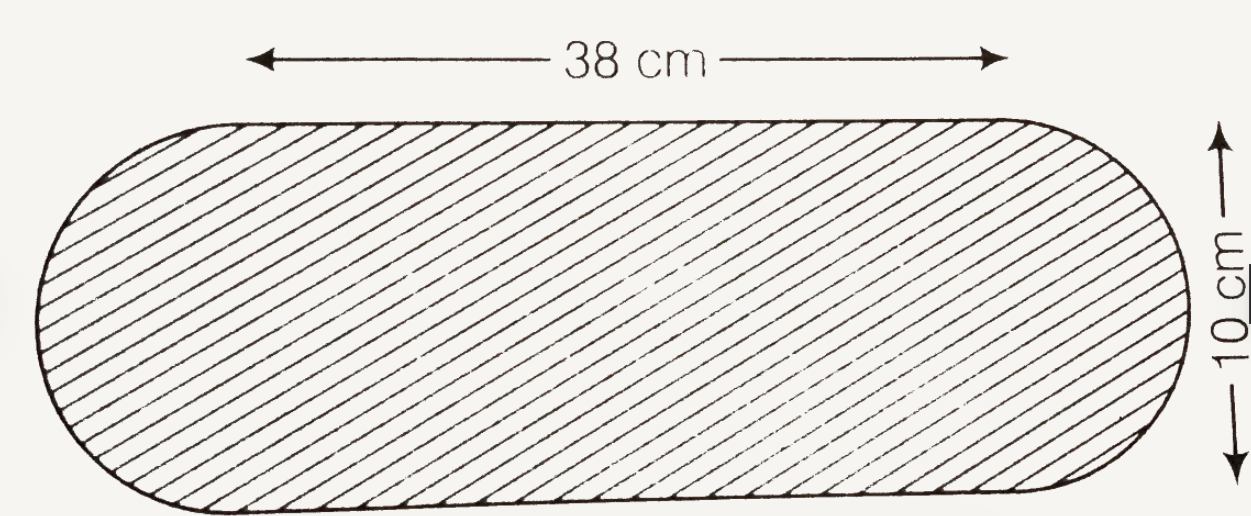
Find the area of the shaded field shown in figure.

Each side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.

Find the number of maxima attend on circular perimeter as shown in the figure. Assume radius of circle gt gt gt lamda . .

Find the area of the shape shown in the figure 10.10.

A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order for the total surface area to be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is pi:(pi+2) .

A plot is in the form of a rectangle A B C D having semi-circle on B C as shown in Figure. If A B=60 m\ a n d\ B C=28 c m , find the area of the plot.