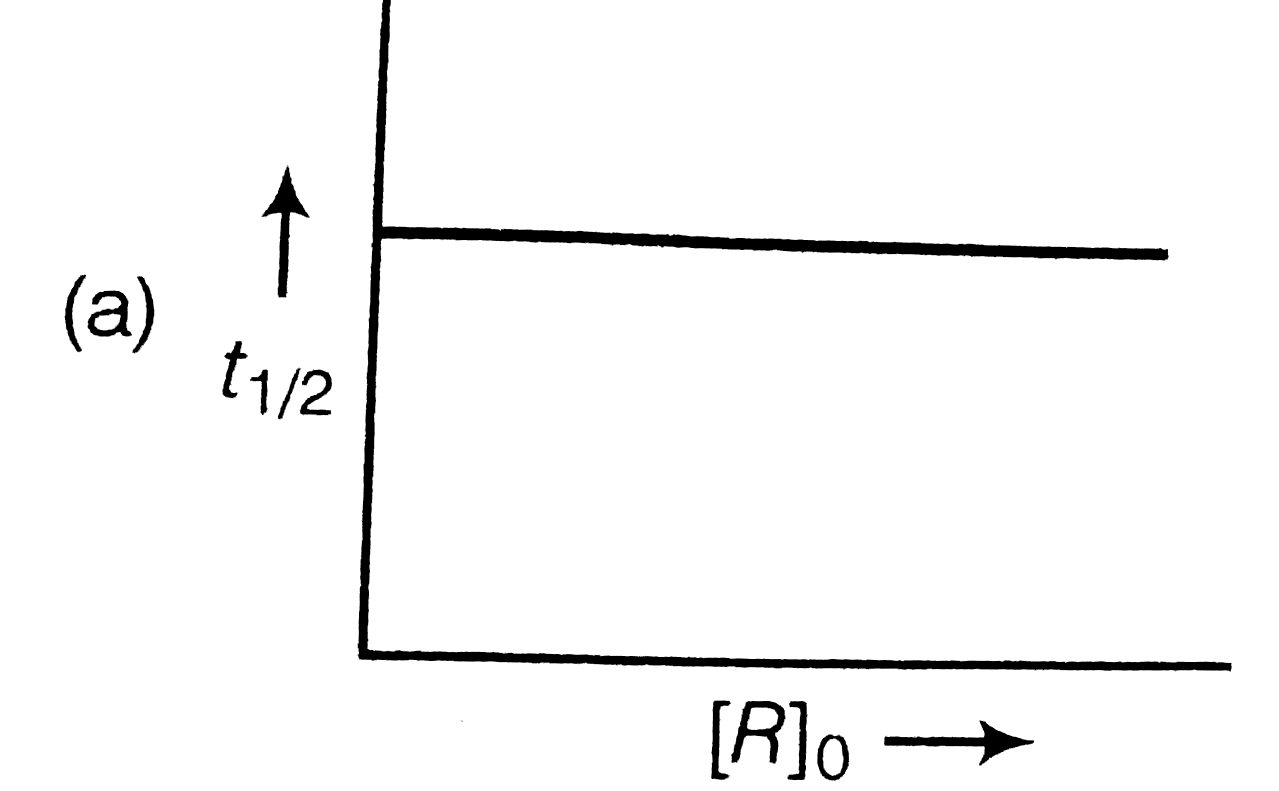
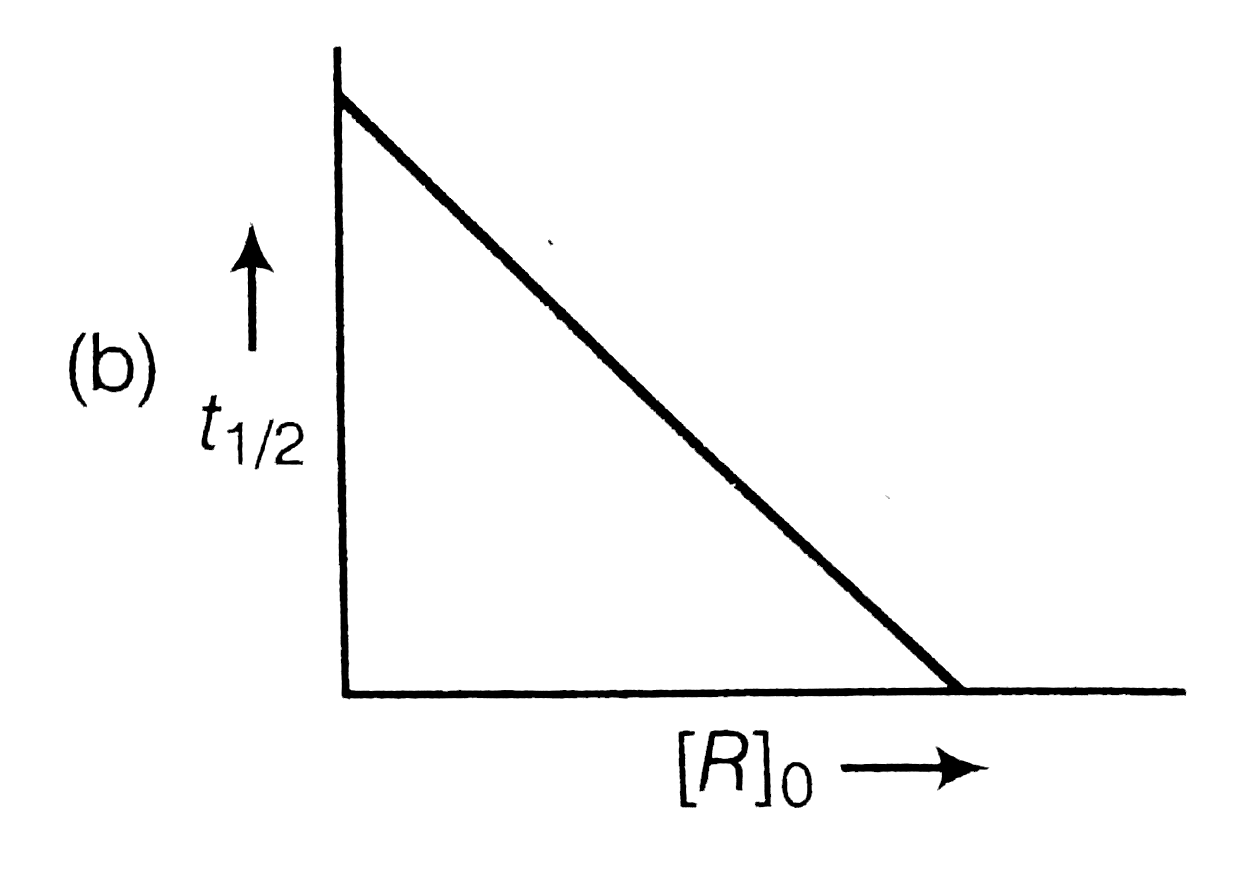
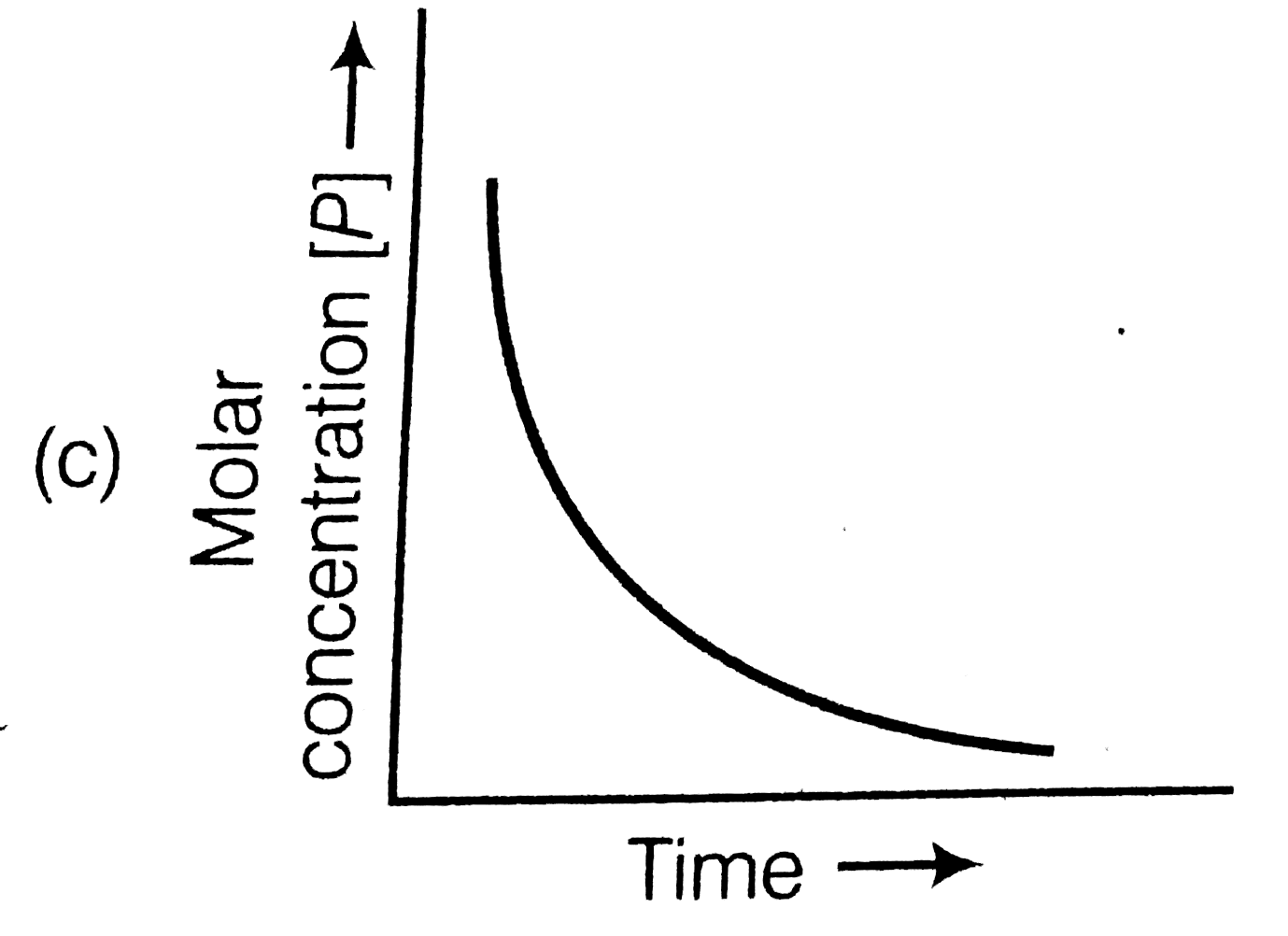
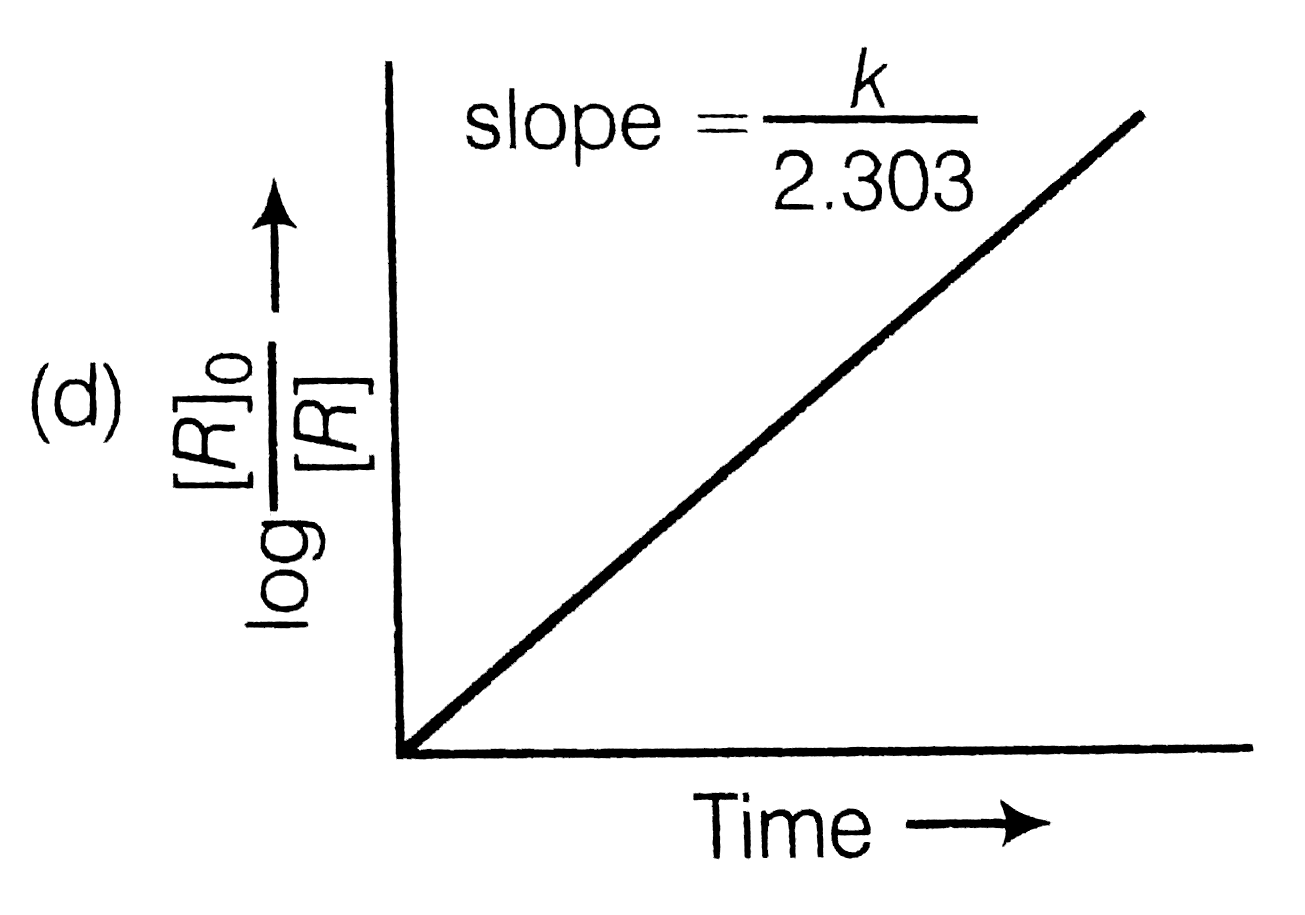
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CHEMICAL KINETICS
NCERT EXEMPLAR ENGLISH|Exercise SHORT ANSWER TYPE QUESTION|20 VideosCHEMICAL KINETICS
NCERT EXEMPLAR ENGLISH|Exercise MATCHING THE COLUMNS|9 VideosCHEMICAL KINETICS
NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPE QUESTIONS|5 VideosBIOMOLECULES
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|5 VideosCHEMISTRY IN EVERYDAY LIFE
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Qns|4 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-CHEMICAL KINETICS-MULTIPLE CHOICE QUESTIONS
- Rate law cannot be determined form balanced chemical equation if â...
Text Solution
|
- Which of the following statements are applicable to a balanced chem...
Text Solution
|
- In any unimoelcular reaction ……. .
Text Solution
|
- For a complex reaction ……… .
Text Solution
|
- At high pressure the following reaction is zero order. " "2N...
Text Solution
|
- During decomposition of an activated complex
Text Solution
|
- According to Maxwell , Boltzmann distriubtion of energy ……… .
Text Solution
|
- In the graph showing Maxwell, Boltzmann distribution of energy â...
Text Solution
|
- Which of the following statements are in accordance with the Arrheeniu...
Text Solution
|
- Mark the incorrent statements.
Text Solution
|
- Which of the following graph is correct for a zero order reaction ...
Text Solution
|
- Which of the following graph is correct for a first order reaction ...
Text Solution
|