A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Objective Type Questions
- The area of the region bounded by the curve y=sqrt(16-x^(2)) and X-axi...
Text Solution
|
- Find the area of the region in the first quadrant enclosed by the y-ax...
Text Solution
|
- Area of the regionbounded by the curve y = "cos" x between x = 0 and x...
Text Solution
|
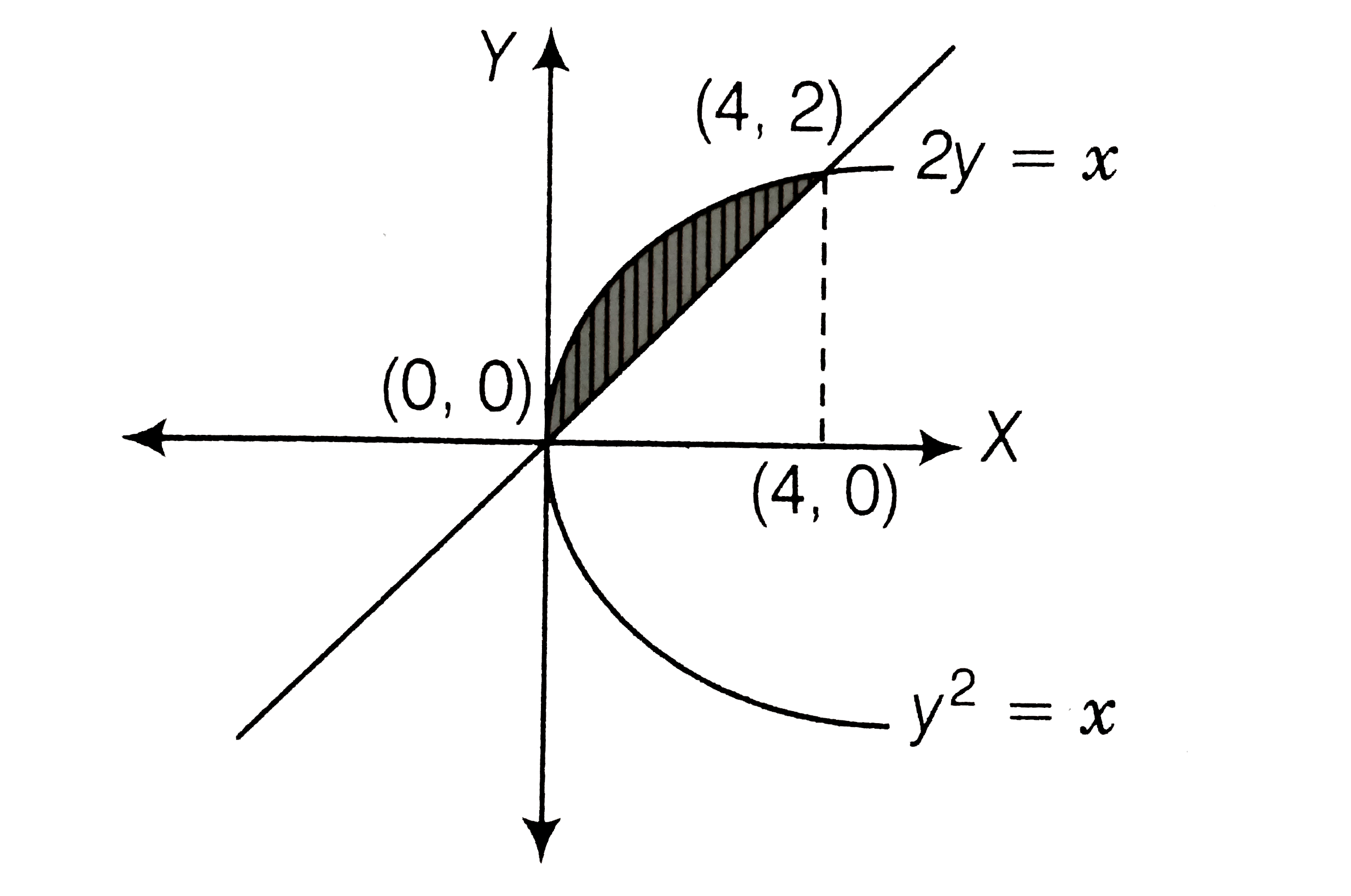
- The area of the region bounded by parabola y^(2)=x and the straight li...
Text Solution
|
- The area of the region bounded by the curve y = "sin" x between the or...
Text Solution
|
- The area of the region bounded by the ellipse (x^(2))/25+y^(2)/16=1 is
Text Solution
|
- The area of the region by the circle x^(2)+y^(2)=1 is
Text Solution
|
- The area of the region bounded by the curve y = x + 1 and the lines x=...
Text Solution
|
- The area of the region bounded by the curve x=2y+3 and the lines y=1, ...
Text Solution
|
- The area of the region bounded by the Y-"axis" y = "cos" x and y = "si...
Text Solution
|
- Using integration, find the area bounded by the curve x^2=4y and the l...
Text Solution
|
- The area of the region bounded by the curve y=sqrt(16-x^(2)) and X-axi...
Text Solution
|
- Area of the region in the first quadrant exclosed by the X-axis, the l...
Text Solution
|
- Area of the regionbounded by the curve y = "cos" x between x = 0 and x...
Text Solution
|
- The area of the region bounded by parabola y^(2)=x and the straight li...
Text Solution
|
- The area of the region bounded by the curve y = "sin" x between the or...
Text Solution
|
- The area of the region bounded by the ellipse (x^(2))/25+y^(2)/16=1 is
Text Solution
|
- The area of the region by the circle x^(2)+y^(2)=1 is
Text Solution
|
- The area of the region bounded by the curve y = x + 1 and the lines x=...
Text Solution
|
- The area of the region bounded by the curve x=2y+3 and the lines y=1, ...
Text Solution
|