Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Long Answer Type Question
- Answer the following: (a) State Gauss' law. Using this law, obtain t...
Text Solution
|
- Two point charges +Q each have been placed at the positions (-a//2,0,0...
Text Solution
|
- A parallel plate capacitor is filled by a dielectric whose relative p...
Text Solution
|
- A capacitor is made of two circular plates of radius R each, separated...
Text Solution
|
- (a) In a quark model of elementary particles, a neutron is made of one...
Text Solution
|
- Two metal spheres, one fo radius R and the other of radius 2R, both ...
Text Solution
|
- In the circuit shown in Fig, initially K(1) is closed and K(2) is open...
Text Solution
|
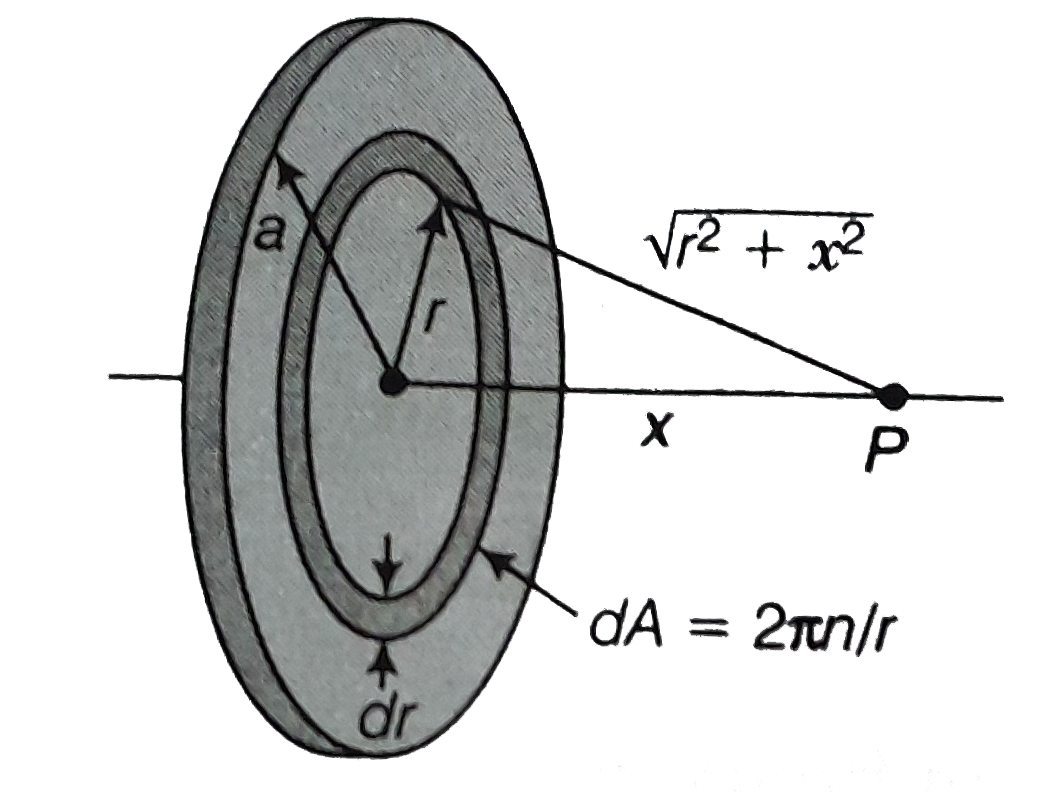
- Calculate potential on the axis of a ring due to charge Q uniformly di...
Text Solution
|
- Two charges q(1) and q(2) are placed at (0,0,d) and (0,0,-d) respectiv...
Text Solution
|
- Two equal charges q are placed at a distance of 2a and a third charge ...
Text Solution
|