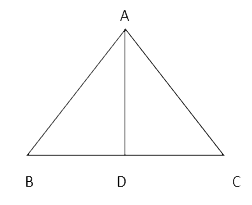
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In an equilateral triangle, prove that three times the square of one s...
Text Solution
|
- In an equilateral triangle, prove that three times the square of one ...
Text Solution
|
- Prove that three times the square of any side of an equilateral-tri...
Text Solution
|
- Prove that in an equilateral triangle, three times the square of a ...
Text Solution
|
- Prove that three times the sum of the squares on the sides of a triang...
Text Solution
|
- In an equilateral triangle, prove that three times the square of one s...
Text Solution
|
- किसी समबाहु त्रिभुज में , सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिग...
Text Solution
|
- किसी समबाहु त्रिभुज में , सिद्ध कीजिए कि उसकी एक भुजा के वर...
Text Solution
|
- सिद्ध कीजिए कि त्रिभुज कि भुजाओ के वर्गों के योगफल का तीन गुना त्रिभुज...
Text Solution
|