Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-APPLICATION OF INTEGRALS-All Questions
- The area bounded by the x-axis, the curve y=f(x), and the lines x=1,x=...
Text Solution
|
- A particle moves along x-axis such that its position veries with time ...
Text Solution
|
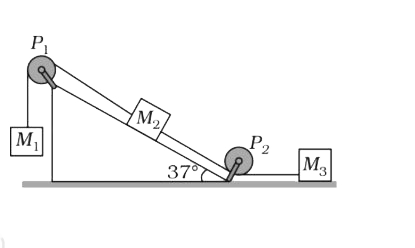
- Masses M(1), M(2) and M(3) are connected by strings of negligible mass...
Text Solution
|
- The area bounded by the two branches of curve (y-x)^2=x^3 and the stra...
Text Solution
|
- The area bounded by the curves y=loge x and y=(loge x)^2 is (A) ...
Text Solution
|
- The area of the region containing the points (x , y) satisfying 4lt=x^...
Text Solution
|
- Let f(x)=x^3+3x+2a n dg(x) be the inverse of it. Then the area bound...
Text Solution
|
- Consider two curves C1: y^2=4[sqrt(y)]x a n dC2: x^2=4[sqrt(x)]y , whe...
Text Solution
|
- The area enclosed between the curve y^2(2a-x)=x^3 and the line x=2a ab...
Text Solution
|
- The area of the region of the plane bounded by max(|x|,|y|)lt=1 and x ...
Text Solution
|
- The area of the figure bounded by the parabola (y-2)^(2)=x-1, the tang...
Text Solution
|
- The area of the loop of the curve a y^2=x^2(a-x) is
Text Solution
|
- The area of the region bounded by x=0,y=0,x=2,y=2,ylt=e^x and ygeq1nx ...
Text Solution
|
- If f(x)=sinx ,AAx in [0,pi/2],f(x)+f(pi-x)=2,AAx in (pi/2,pi]a n df(x)...
Text Solution
|
- The area enclosed by the curve y=sqrt(4-x^2),ygeqsqrt(2)sin((xpi)/(2sq...
Text Solution
|
- The area bounded by the curves y=xe^x,y=xe^-x and the lines x=1 is
Text Solution
|
- The area enclosed by the curves xy^2=a^2(a-x) and (a-x)y^2=a^2x is
Text Solution
|
- The area bounded by the loop of the curve 4y^2=x^2(4-x^2) is (a)7/3 sq...
Text Solution
|
- The area bounded by the curve f(x)=x+sinx and its inverse function bet...
Text Solution
|
- The area enclosed by the curve y=sinx+cosxa n dy=|cosx-sinx| over the ...
Text Solution
|