Home
Class 12
MATHS
Consider the function f(x)={{:(x-[x]-(1)...

Consider the function `f(x)={{:(x-[x]-(1)/(2),x !in),(0, "x inI):}` where [.] denotes the fractional integral function and I is the set of integers. Then find `g(x)max.[x^(2),f(x),|x|},-2lexle2.`

Text Solution

Verified by Experts

We first draw the graphs of `y=f(x),y=x^(2)andy=|x|``y=f(x),y=x^(2)andy=|x|`.
To deaw the graph of `y=x-[x]-0.5={x}-0.5`, we shift the graph of `y={x},0.5` units downward vertically for non-nitegral values of x and plotting '0' for integral values fo x as shown in the following in the following figure.

Clearly, from the graph, g(.x) =`{{:(x^(2)",",-2lexle-1),(1-x",",-1lexle-1//4),((1)/(2)+x",",-(1)/(4)ltxlt0),(1+x",",0lexle1),(x^(2)",",1lele2):}`
Promotional Banner

Topper's Solved these Questions

  • GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE ENGLISH|Exercise Exercises|18 Videos

  • GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS

    CENGAGE ENGLISH|Exercise Exercises|17 Videos

Similar Questions

Explore conceptually related problems

if f(x) ={{:(2x-[x]+ xsin (x-[x]),,x ne 0) ,( 0,, x=0):} where [.] denotes the greatest integer function then

The domain of function f (x) = log _([x+(1)/(2)])(2x ^(2) + x-1), where [.] denotes the greatest integer function is :

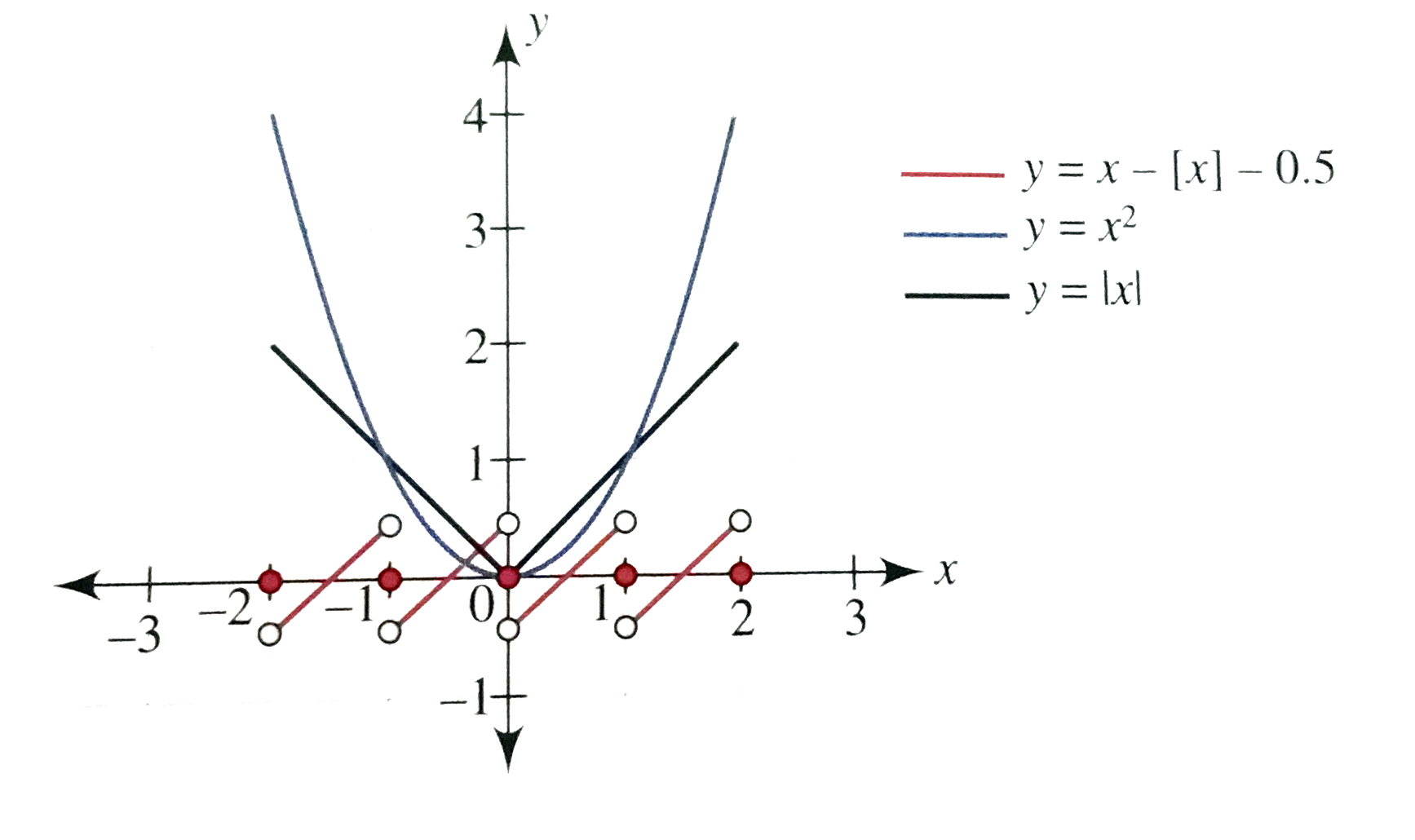
Consider the function f(x)={(x-[x]-1/2, if x!inI),(0, if x!inI):} where [.] denotes the greatest integer function and g(x)=max. {x^2, f(x), |x|}, -2 le x le 2 . Now answer the question:Area bounded by y=g(x) when -2 le x le 2 is (A) 175/48 (B) 275/48 (C) 175/24 (D) 275/24

The function f(x)=[x]^(2)+[-x^(2)] , where [.] denotes the greatest integer function, is

If f(x)=([x])/(|x|),x ne 0 where [.] denotes the greatest integer function, then f'(1) is

The function f(x)=[x]+1/2,x!inI is a/an (wher [.] denotes greatest integer function)

If f(x)=([x])/(|x|), x ne 0 , where [.] denotes the greatest integer function, then f'(1) is

If f(x)={{:(e^(|x|+|x|-1)/(|x|+|x|),":",xne0),(-1,":",x=0):} (where [.] denotes the greatest integer integer function), then

f(x)=sin^-1[log_2(x^2/2)] where [ . ] denotes the greatest integer function.

The function f(x) = [x] cos((2x-1)/2) pi where [ ] denotes the greatest integer function, is discontinuous