A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise LINKED COMPREHENSION TYPE|12 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise MATRIX-MATCH TYPE|5 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise MULTIPLE CORRECT ANSWER TYPE|17 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise All Questions|294 VideosTRIGONOMETRIC EQUATIONS
CENGAGE ENGLISH|Exercise Archives (Matrix Match Type)|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-THREE-DIMENSIONAL GEOMETRY -REASONING TYPE
- Statement 1 : Lines vecr= hati-hatj+ lamda (hati+hatj-hatk) and vecr= ...
Text Solution
|
- Statement 1 : Lines vecr=hati+hatj-hatk+lamda(3hati-hatj) and vecr=4ha...
Text Solution
|
- The equation of two straight lines are (x-1)/2=(y+3)/1=(z-2)/(-3)a n...
Text Solution
|
- Statement 1: A plane passes through the point A(2,1,-3)dot If distan...
Text Solution
|
- Statement 1: Line (x-1)/1=(y-0)/2=(z+2)/(-1) lies in the plane 2x-3y-4...
Text Solution
|
- Statement 1: Let theta be the angle between the line (x-2)/2=(y-1)/(-3...
Text Solution
|
- Statement 1: let A( vec i+ vec j+ vec k)a n dB( vec i- vec j+ vec k) b...
Text Solution
|
- Statement 1: there exists a unique sphere which passes through the ...
Text Solution
|
- Statement 1: There exist two points on the (x-1)/1=y/(-1)=(z+2)/2 w...
Text Solution
|
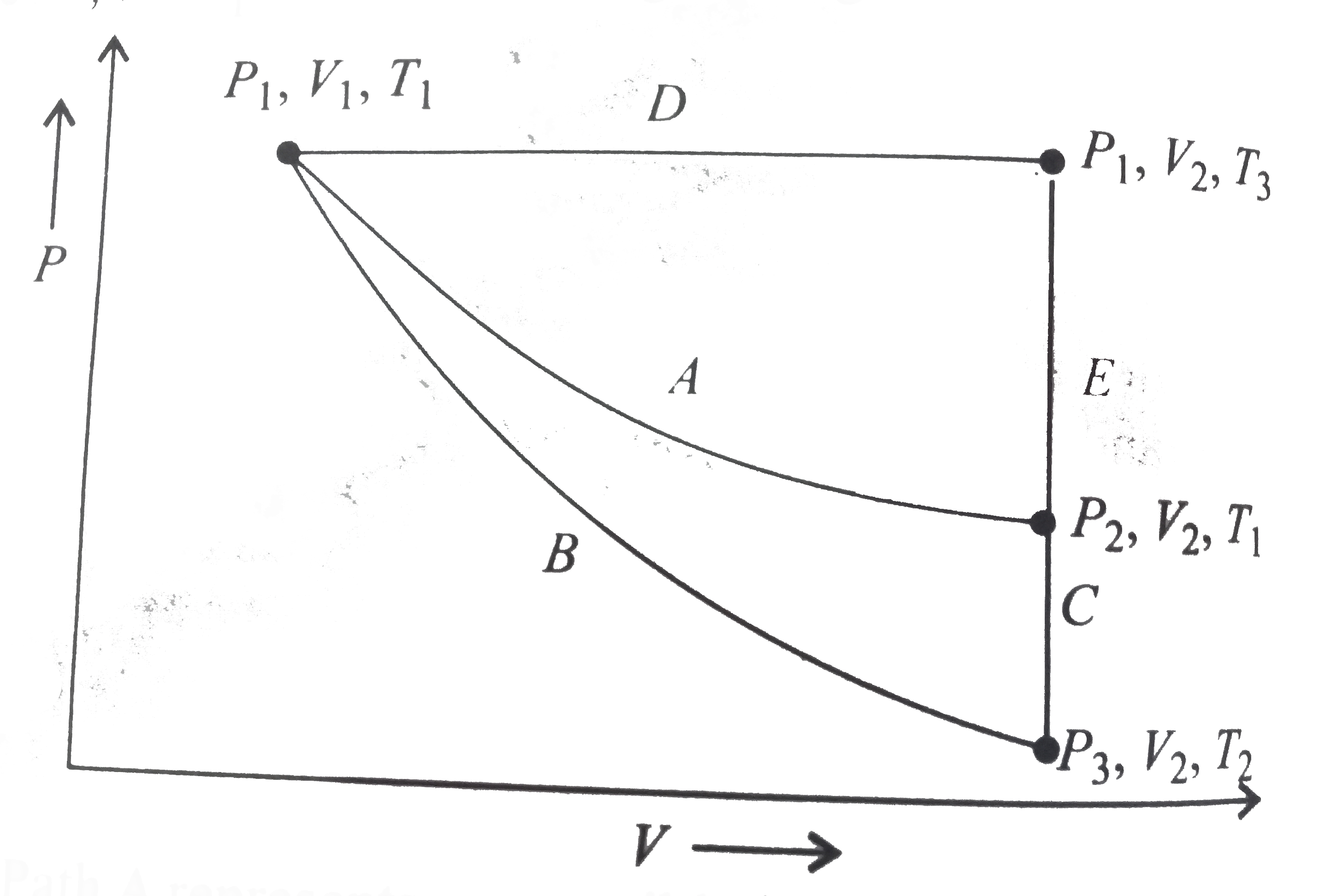
- For an ideal gas, an illustration of three different paths A(B+C) and ...
Text Solution
|