A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise MATRIX-MATCH TYPE|5 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise INTEGER TYPE|10 VideosTHREE-DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise REASONING TYPE|10 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise All Questions|294 VideosTRIGONOMETRIC EQUATIONS
CENGAGE ENGLISH|Exercise Archives (Matrix Match Type)|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-THREE-DIMENSIONAL GEOMETRY -LINKED COMPREHENSION TYPE
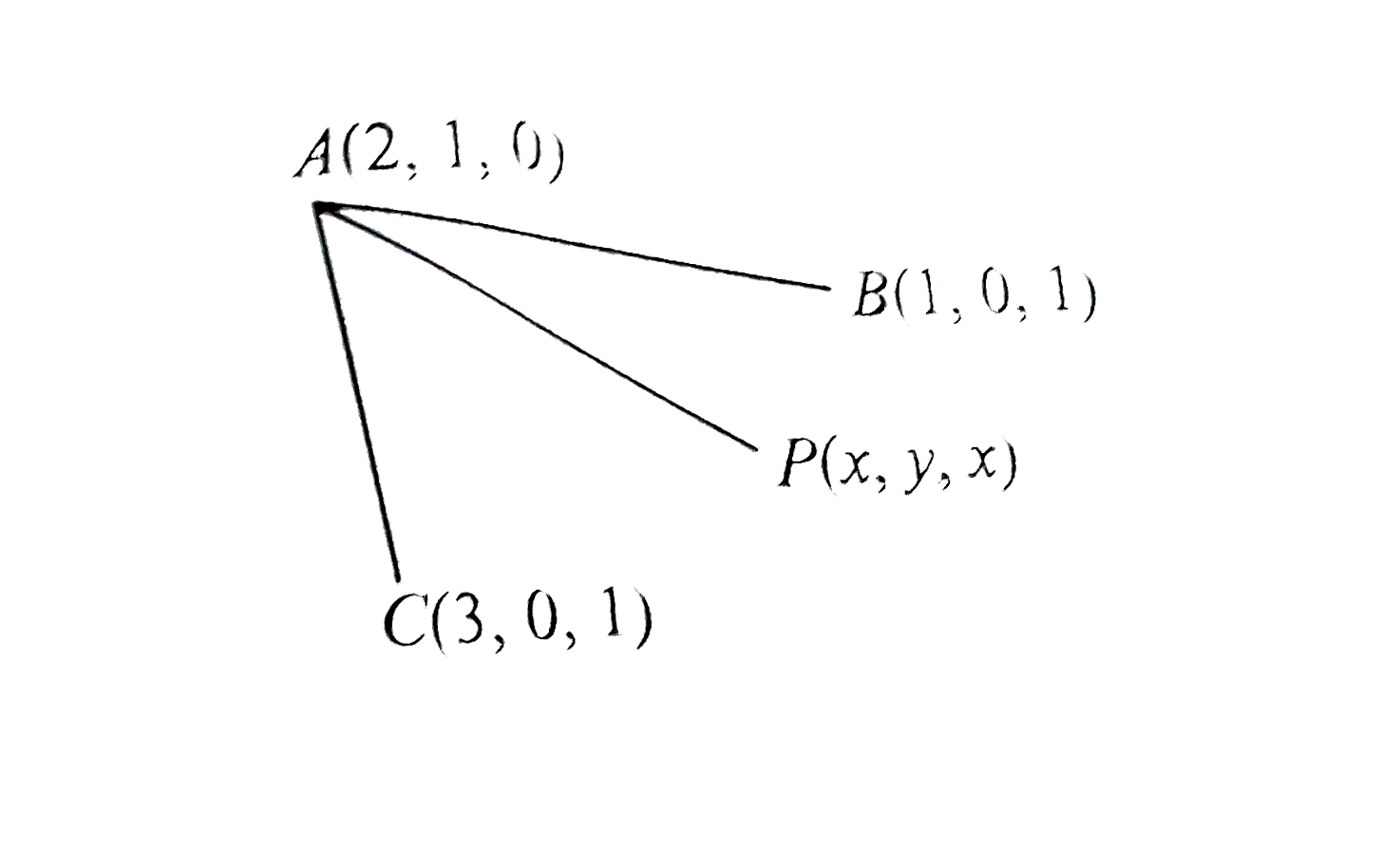
- Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
Text Solution
|
- Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
Text Solution
|
- Given four points A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) and D(0, 0, 2). P...
Text Solution
|
- A ray of light comes light comes along the line L = 0 and strikes the ...
Text Solution
|
- A ray of light comes light comes along the line L = 0 and strikes the ...
Text Solution
|
- A ray of light comes light comes along the line L = 0 and strikes the ...
Text Solution
|
- For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
Text Solution
|
- For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
Text Solution
|
- For what values of p and q the system of equations 2x+py+6z=8, x+2y+qz...
Text Solution
|
- Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
Text Solution
|
- Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
Text Solution
|
- Consider a plane x+y-z=1 and point A(1, 2, -3). A line L has the equat...
Text Solution
|