The given line and plane are `vecr= (2hati-2hatj+3hatk)+lamda(hati-hatj+4hatk) and vecr*(hati+5hatj+hatk)=5`, respectively. Since `(hati-hatj+4hatk)*(hati+5hatj+hatk)=0`, line and plane are parallel.
Hence, the required distance is equal to distance of point `(2, -2, 3)` from the plane `x+5y+z-5=0`, which is `(|2-10+3-5|)/(sqrt(1+25+1))= (10)/(3sqrt(3))`
b. The distance between two parallel planes `vecr*(2i-j+3k)=4 and vecr*(6i-3j+9k)+13=0` is
`" "d= (|4-(-13//3)|)/(sqrt((2)^(2)+ (-1)^(2)+ (3)^(2))) = ((25//3))/(sqrt(14))`
`" "=(25)/(3sqrt(14))`
c. The perpendicular distance of the point `(2, 5, -3)` fromt the plane `vecr*(6i-3j+2k)=4 or 6x-3y+2z-4=0` is
`" "d= (|12-15-6-4|)/(sqrt(36+9+4))`
`" "=13//sqrt(49)= 13//7`
d. The equation of the line `AB` is
`" "(x-2)/(2)= (y+2)/(3)= (z-6)/(-6)`
The equation of line passing through `(1, 0, -3)` and parallel to `AB` is
`" "(x-1)/(2)= (y)/(3)= (z+3)/(-6)= r` (say)
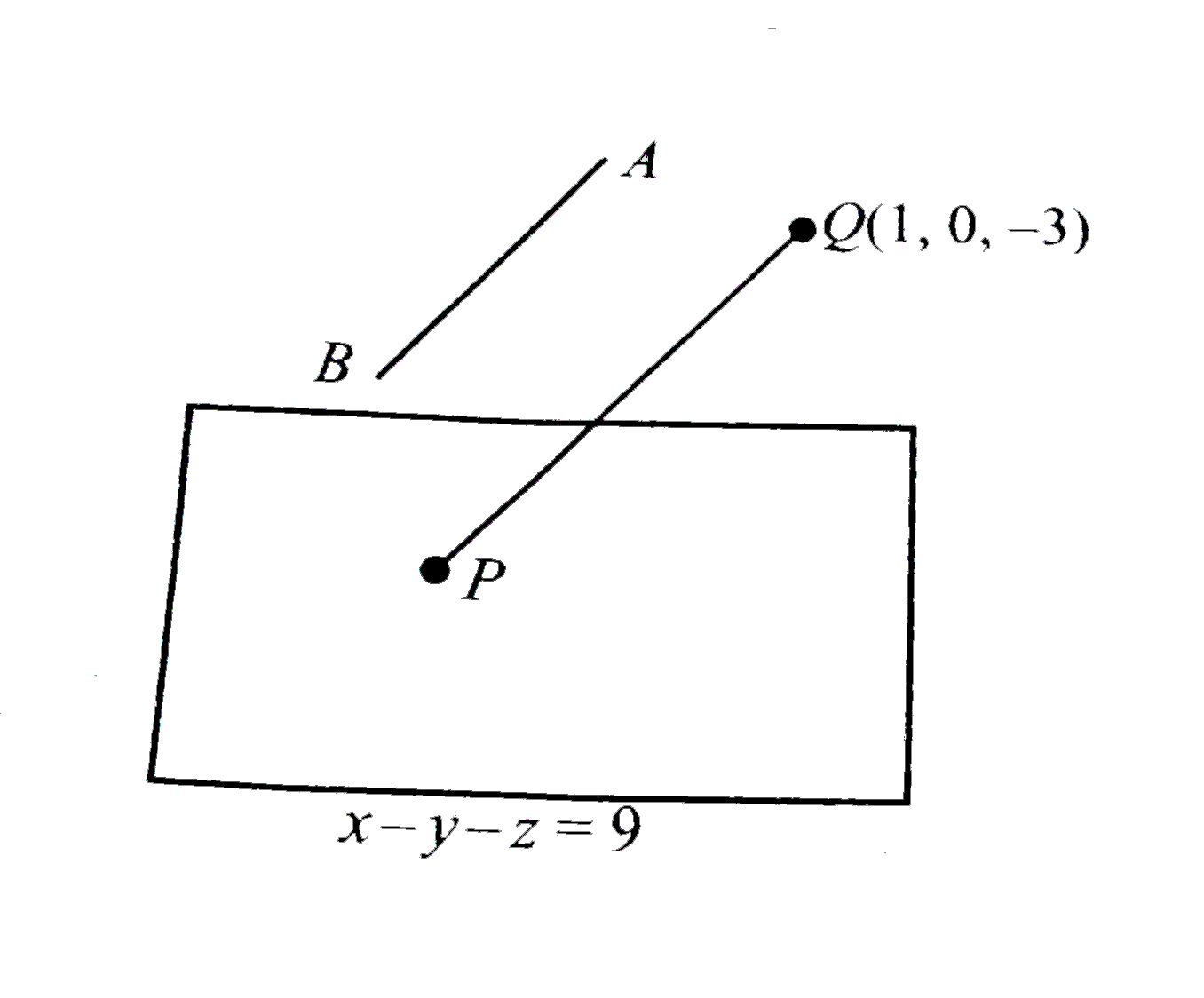
The coordinates of any point on line `P(2r+1, 3r, -6r-3)` which lie on plane
`" "(2r+1)- (3r)- (-6r-3)=9`
`" "r=1`
Point `P-= (3, 3, -9)`
Required distance
`" "PQ= sqrt((3-1)^(2)+ (3-0)^(2)+ (-9+3)^(2))`
`" "=sqrt(4=9+36)= 7`