Home
Class 12
MATHS
Draw the graph of the function f(x)= x- ...

Draw the graph of the function `f(x)= x- |x-x^(2)|, -1 le x le 1` and find the points of non-differentiability.

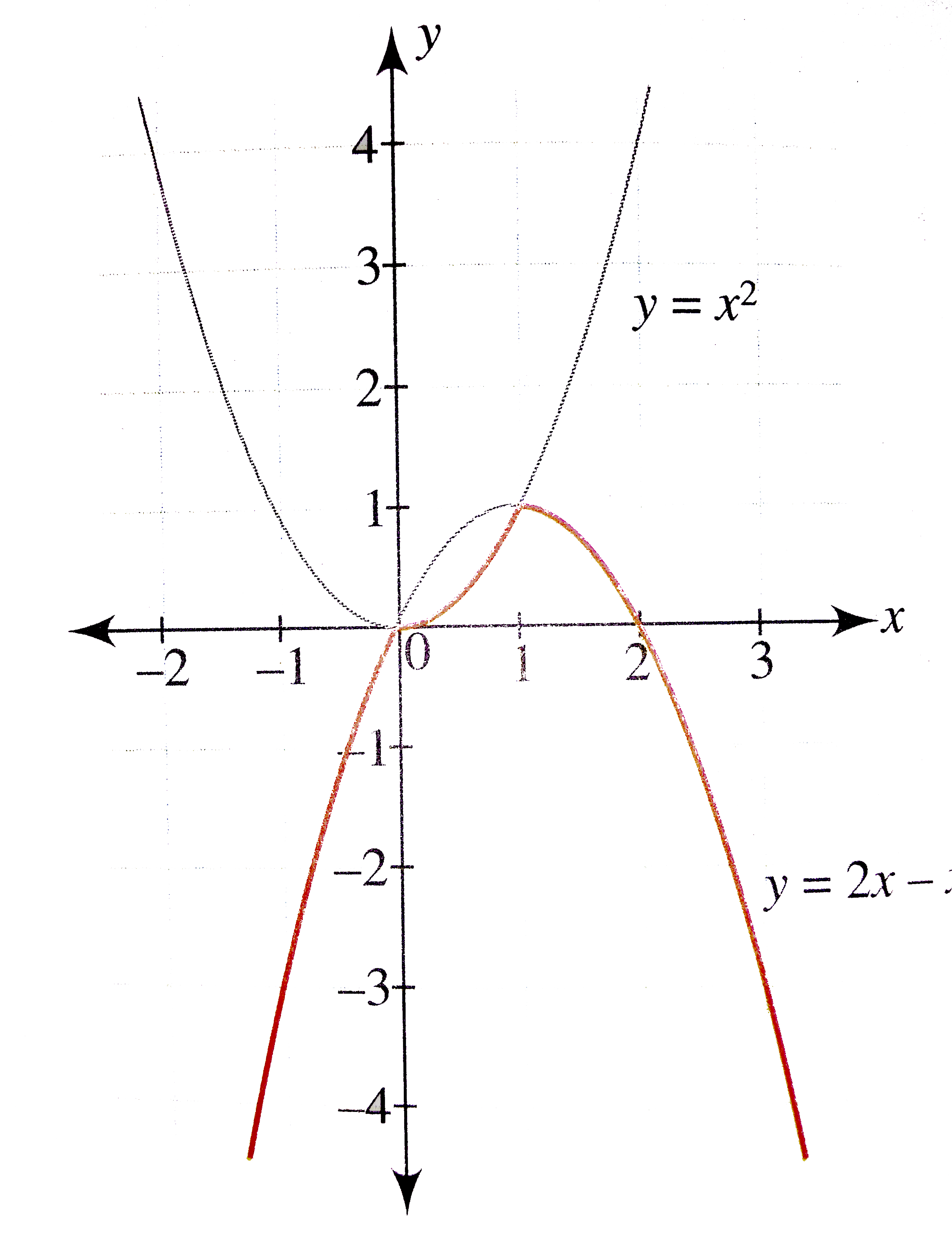
Text Solution

Verified by Experts

We have `y= f(x)=x- |x-x^(2)|`
`" "= {{:(x-(x^(2)-x)",",,x^(2)-x ge0),(x-(x-x^(2))",",,x^(2)-x lt 0):}`
`" "= {{:(x-(2x-x^(2))",",,xle0 or x ge 1),(x^(2)",",,0ltxlt1):}`
The graph of the function `y= 2x-x^(2)= x(2-x)` is a downward parabola intersecting the x-axis at `x=0 and x=2`.
Thus, the graph of the function `y= f(x)` is as follows:

Clearly from the graph the function is continuous but non-differentiable at `x=0, 1`.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • GRAPHS OF ELEMENTARY FUNCTIONS

    CENGAGE ENGLISH|Exercise EXERCISES|34 Videos

  • GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS

    CENGAGE ENGLISH|Exercise Exercises|17 Videos

  • GRAPHS OF TRIGONOMETRIC FUNCTIONS

    CENGAGE ENGLISH|Exercise Exercises|22 Videos

Similar Questions

Explore conceptually related problems

Draw the graph of the function f(x)=|x-1|

Draw the graph of the function: f(x)=-|x-1|^(1/2)

Draw the graph of the function f(x) = (1+1/x)^(2)

Draw the graph of the function f(x) = x - |x - x^(2)|, -1 le x le 1 and discuss the continuity or discontinuity of f in the interval -1 le x le 1

The range of the function f(x)=|x-1|+|x-2|, -1 le x le 3, is

Redefine the function f(x)= |1+x| +|1-x|, -2 le x le 2 .

Draw the graph of the function f(x) = x-|x2-x| -1 le x le 1 , where [*] denotes the greatest integer function. Find the points of discontinuity and non-differentiability.

Drew the graph of the function and find the points of non-differentiability .(i) f(x) = min ,{x, sin x}.

f(x)=abs(x-1)+abs(x-2), -1 le x le 3 . Find the range of f(x).

Draw the graph of f(x) = 2x+3x^(2//3) and discuss the type of non-differentiability for the function. Also find the point of inflection.

Home
Profile