Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise Concept Application Exercises 2.2|8 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise Concept Application Exercises 2.3|4 VideosTRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise example|10 VideosTRIGONOMETRIC EQUATIONS
CENGAGE ENGLISH|Exercise Archives (Matrix Match Type)|1 VideosTRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
CENGAGE ENGLISH|Exercise Matrix Match Type|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-TRIGONOMETRIC FUNCTIONS -Concept Application Exercises 2.1
- Two sides of a parallelgram are 12 cm and 8 cm. If one of the interio...
Text Solution
|
- In triangle ABC, AB=6,AC=3sqrt6,angleB=60^@" and " angle C=45^(@). Fin...
Text Solution
|
- The circumference of a circle circumscribing an equilateral triangle i...
Text Solution
|
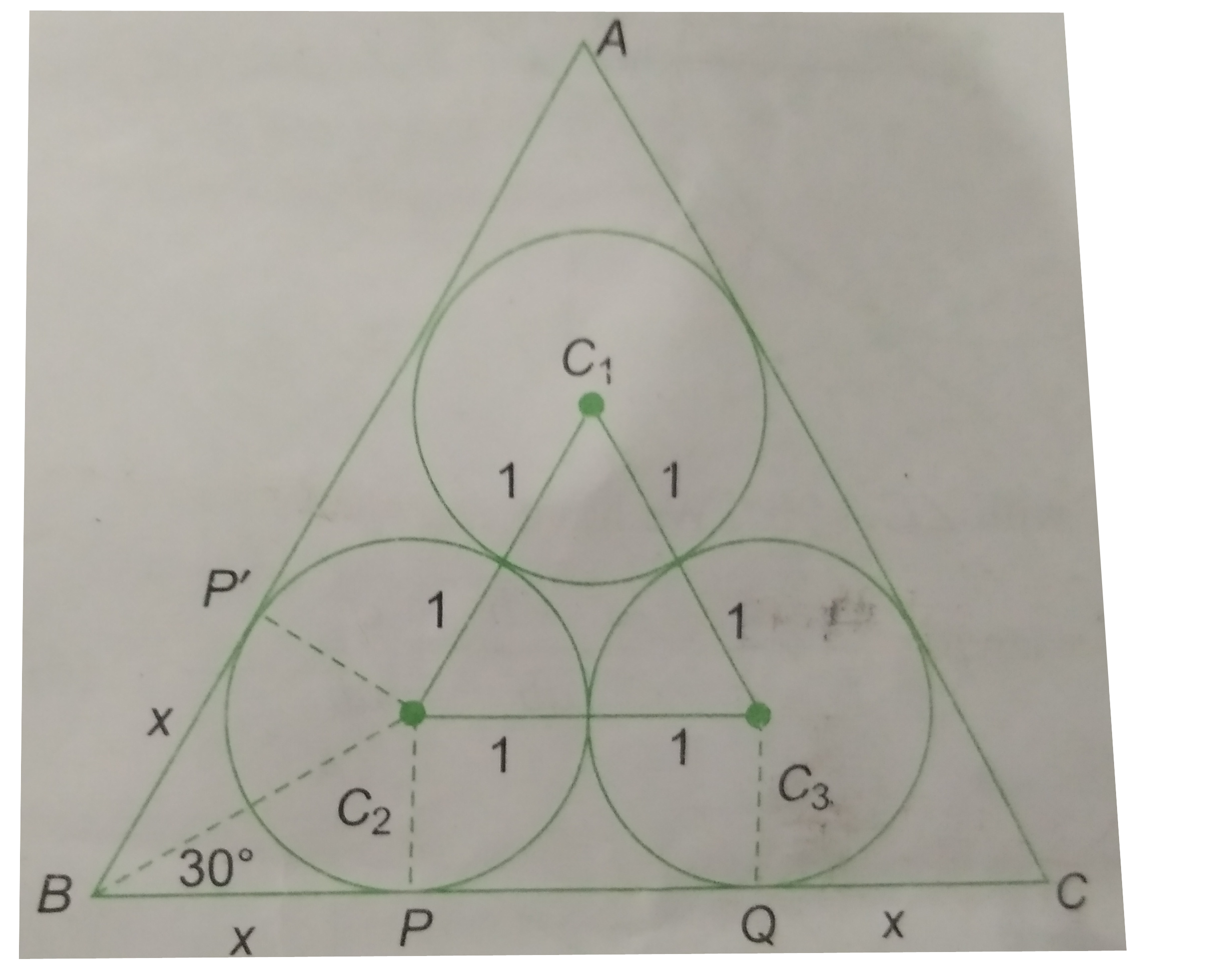
- In an equilateral triangle, three coins of radii 1 unit each are kept ...
Text Solution
|
- A polygon of nine sides, each pf length 2, is inscribed in a circle. P...
Text Solution
|
- Two circles of radii 4cm and 1cm touch each other externally and theta...
Text Solution
|
- If angle C of triangle ABC is 90^0, then prove that tanA+tanB=(c^2)/(a...
Text Solution
|
- If cos^2alpha-sin^2alpha=tan^2beta," then prove that "tan^2alpha=cos^2...
Text Solution
|