Home
Class 12
MATHS
Find the area lying in the first quadran...

Find the area lying in the first quadrant and bounded by the curve `y=x^3` and the line `y=4xdot`

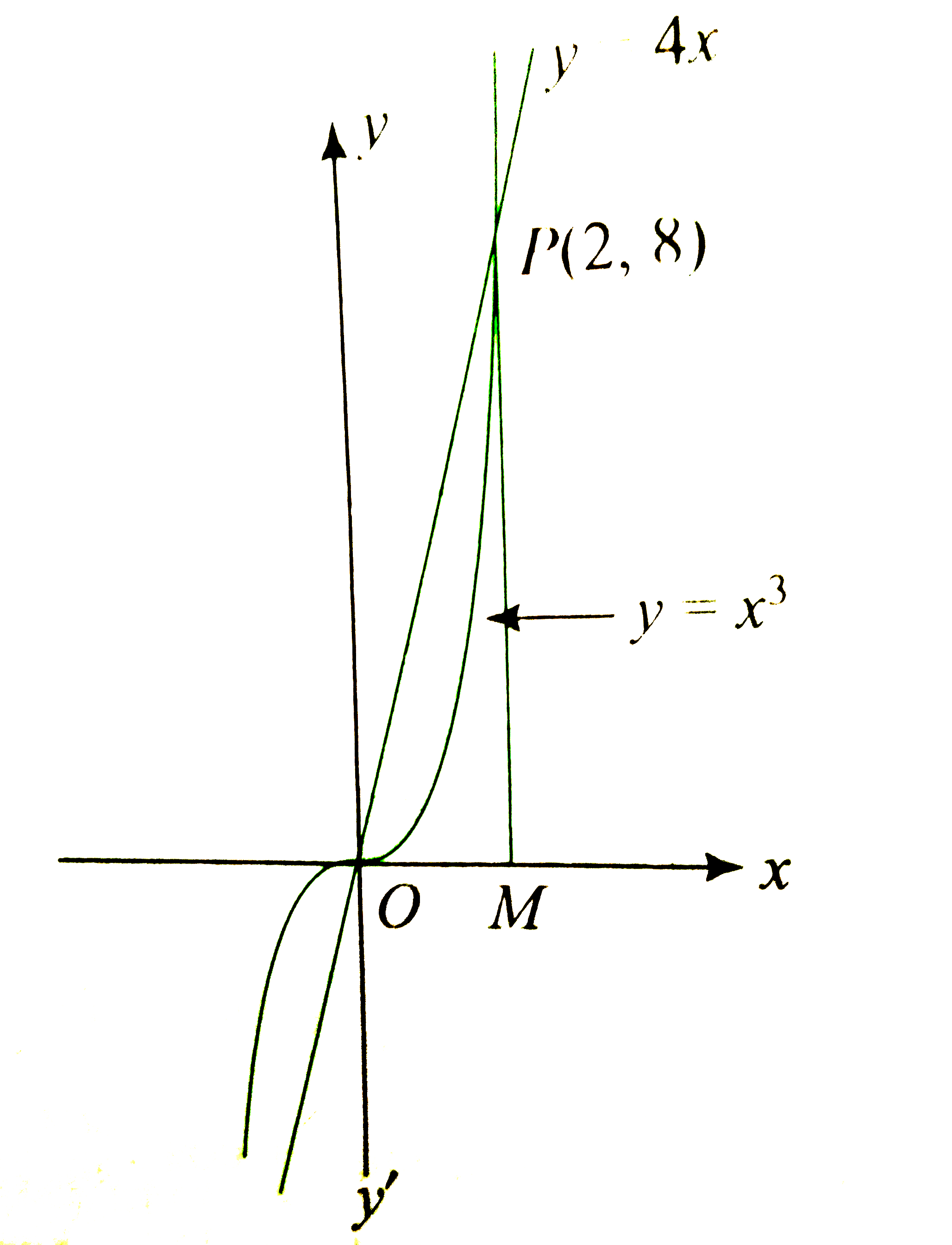
Text Solution

Verified by Experts

The correct Answer is:
4 sq. units
`"The line "y=4x" meets "y=x^(3)" at "4x=x^(3)`.
`therefore" "x=0, 2,-2rArry=0,8,-8`
`rArr" "A=int_(0)^(2)(4x-x^(3))=(2x^(2)-(x^(4))/(4))_(0)^(2)=4` sq. units
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE ENGLISH|Exercise Concept Application Exercise 9.3|7 Videos

  • AREA

    CENGAGE ENGLISH|Exercise Exercises - Single Correct Answer Type|40 Videos

  • AREA

    CENGAGE ENGLISH|Exercise Concept Application Exercise 9.1|9 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE ENGLISH|Exercise Comprehension Type|5 Videos

  • BINOMIAL THEOREM

    CENGAGE ENGLISH|Exercise Matrix|4 Videos

Similar Questions

Explore conceptually related problems

Find the area of the figure lying in the first quadrant and bounded by the curves y^2=4x, x^2=4y .

Area lying in the first quadrant and bounded by the circle x^2+y^2=4 and the lines x= 0 and x= 2 is:

Area lying in the first quadrant and bounded by the circle x^2+y^2=4 and the lines x= 0 a n dx= 2 is(A) pi (B) pi/2 (C) pi/3 (D) pi/4

Find the area bounded by the curve y=2x-x^(2) , and the line y=x

Find the area bounded by the curves y=2x-x^2 and the straight line y=-xdot

Area lying in the first quadrant and bounded by the circle x^(2)+y^(2)=4 the line x=sqrt(3)y and x-axis , is

Find the area bounded by the curves y=4-x^2 and the lines y=0andy=3

Find the area of the region bounded by the curve y=x^2 and the line y" "=" "4 .

Find the area of the region bounded by the curves y=x^3 and the lines y=x+6 and y=0.

The area bounded by the curve x^(2)=4ay and the line y=2a is