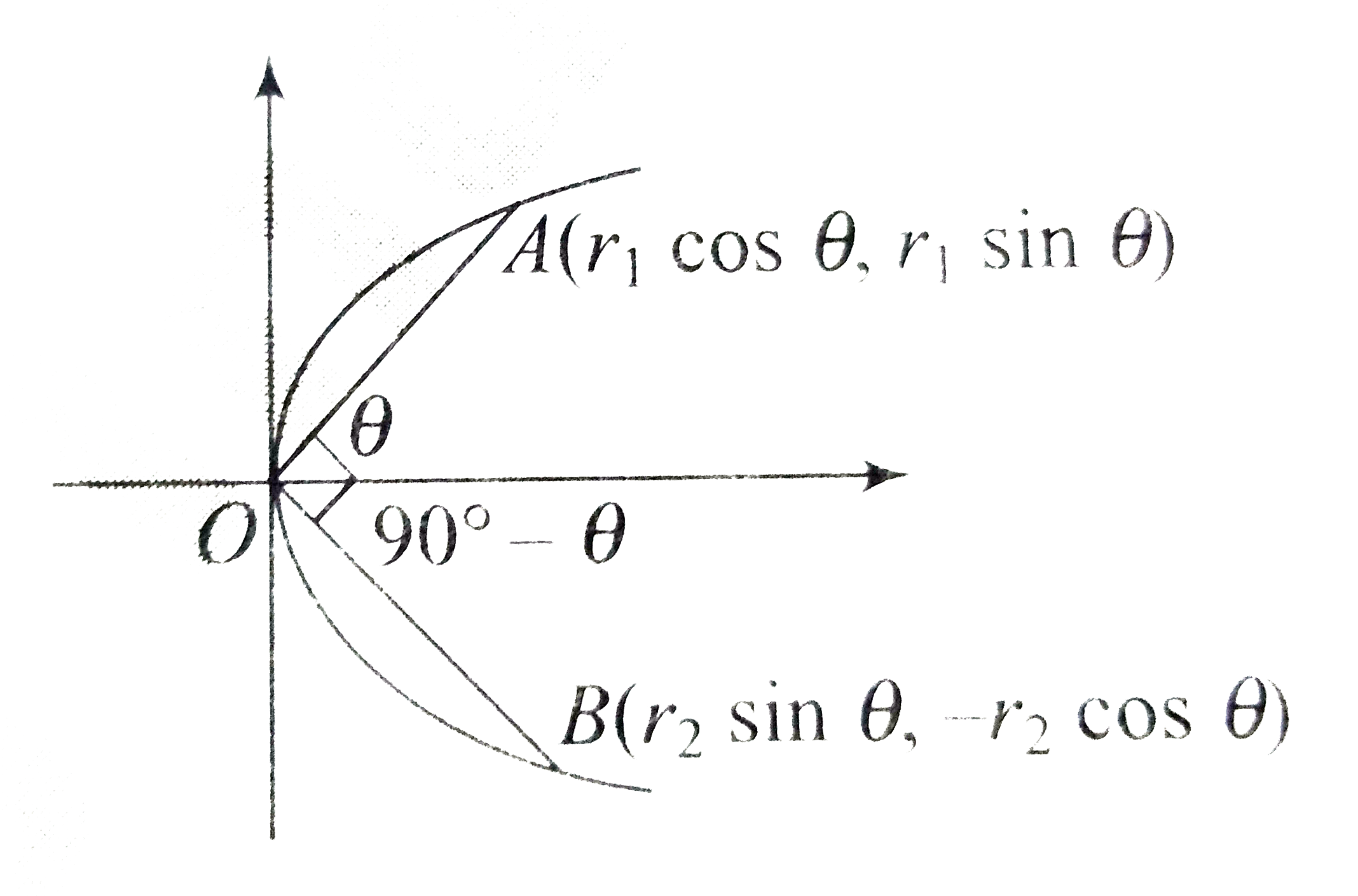A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PARABOLA
CENGAGE ENGLISH|Exercise Multiple Correct Answers Type|10 VideosPARABOLA
CENGAGE ENGLISH|Exercise Comprehension Type|2 VideosPARABOLA
CENGAGE ENGLISH|Exercise MULTIPLE CORRECT ANSWER TYPE|7 VideosPAIR OF STRAIGHT LINES
CENGAGE ENGLISH|Exercise Numberical Value Type|5 VideosPERMUTATION AND COMBINATION
CENGAGE ENGLISH|Exercise Comprehension|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-PARABOLA-Single Correct Answer Type
- Find the equations of the chords of the parabola y^2= 4ax which pass t...
Text Solution
|
- Two equal circles of largest radii have following property: (i) They...
Text Solution
|
- Let P and Q are points on the parabola y^(2)=4ax with vertex O, such t...
Text Solution
|
- A line ax +by +c = 0 through the point A(-2,0) intersects the curve y^...
Text Solution
|
- Suppose a parabola y = x^(2) - ax-1 intersects the coordinate axes at ...
Text Solution
|
- The line x - b +lambda y = 0 cuts the parabola y^(2) = 4ax (a gt 0) at...
Text Solution
|
- If the parabola y=(a-b)x^2+(b-c)x+(c-a) touches x- axis then the line...
Text Solution
|
- A normal to parabola, whose inclination is 30^(@), cuts it again at an...
Text Solution
|
- If (-2,5) and (3,7) are the points of intersection of the tangent and ...
Text Solution
|
- The angle of intersection between the curves x^(2) = 4(y +1) and x^(2)...
Text Solution
|
- The parabolas y^2=4ax and x^2=4by intersect orthogonally at point P(x1...
Text Solution
|
- Sum of slopes of common tangent to y = (x^(2))/(4) - 3x +10 and y = 2 ...
Text Solution
|
- The slope of normal to be parabola y = (x^(2))/(4) -2 drawn through th...
Text Solution
|
- The tangent and normal at the point P(4,4) to the parabola, y^(2) = 4x...
Text Solution
|
- The point on the parabola y^(2) = 8x at which the normal is inclined a...
Text Solution
|
- If two distinct chords of a parabola y^2=4ax , passing through (a,2a) ...
Text Solution
|
- From an external point P , a pair of tangents is drawn to the parabola...
Text Solution
|
- A variable parabola y^(2) = 4ax, a (where a ne -(1)/(4)) being the par...
Text Solution
|
- If X is the foot of the directrix on the a parabola. PP' is a double o...
Text Solution
|
- Let PQ be the latus rectum of the parabola y^2 = 4x with vetex A. Mini...
Text Solution
|