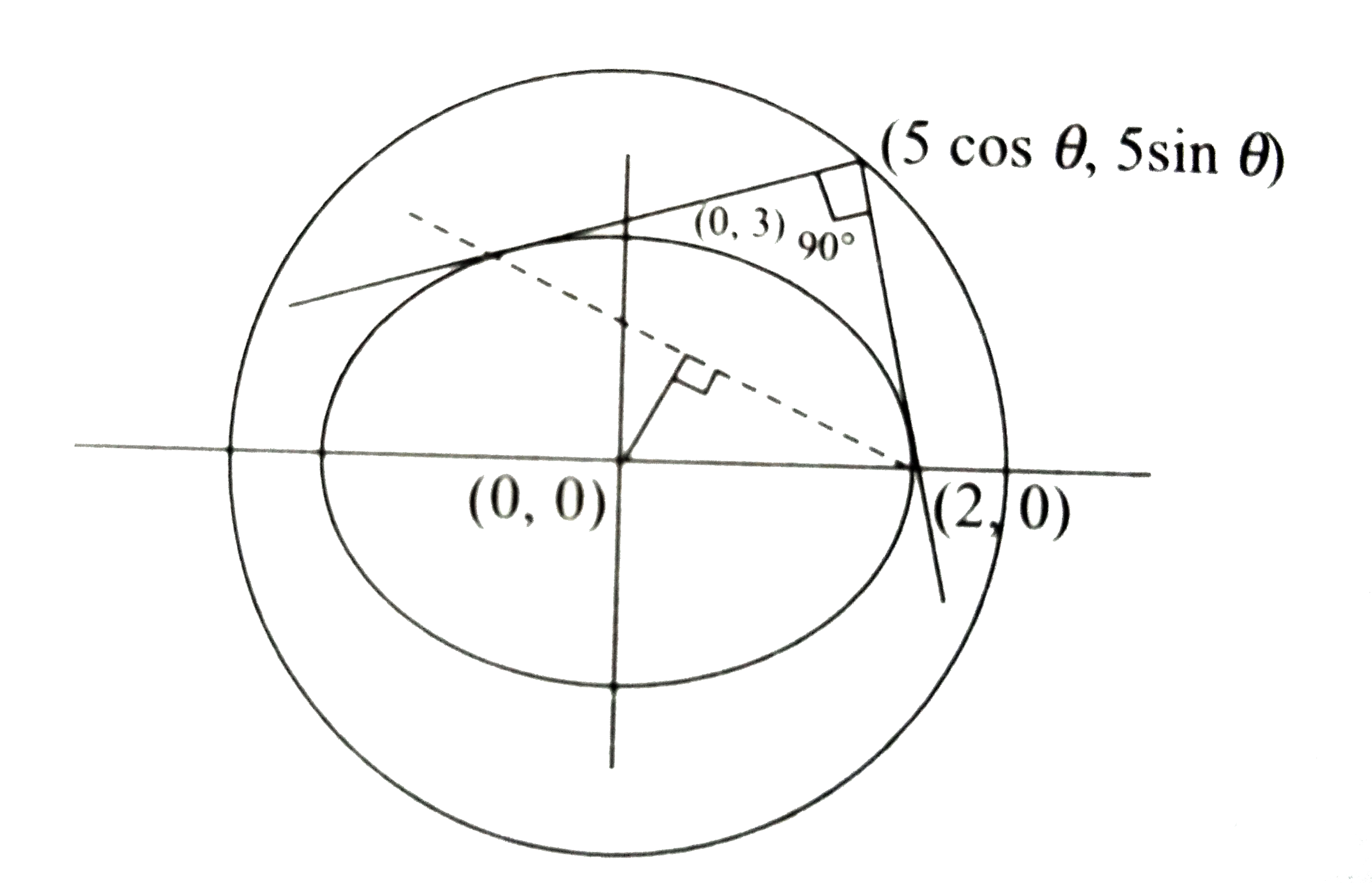
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-ELLIPSE -Single Correct Answer Type
- The tangent at any point on the ellipse 16x^(2)+25y^(2) = 400 meets th...
Text Solution
|
- The minimum value of {(r+5 -4|cos theta|)^(2) +(r-3|sin theta|)^(2)} A...
Text Solution
|
- Let S(1) and S(2) denote the circles x^(2)+y^(2)+10x - 24y - 87 =0 and...
Text Solution
|
- If omega is one of the angles between the normals to the ellipse (x...
Text Solution
|
- From any point on the line (t+2)(x+y) =1, t ne -2, tangents are drawn ...
Text Solution
|
- At a point P on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)) =1 tangent...
Text Solution
|
- From a point P perpendicular tangents PQ and PR are drawn to ellipse x...
Text Solution
|
- If the normal at any point P on ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- Tangents are drawn from any point on the circle x^(2)+y^(2) = 41 to th...
Text Solution
|
- If radius of the director circle of the ellipse ((3x+4y-2)^(2))/(100)+...
Text Solution
|
- If the curve x^(2)+3y^(2)=9 subtends an obtuse angle at the point (2al...
Text Solution
|
- An ellipse has the points (1, -1) and (2,-1) as its foci and x + y = 5...
Text Solution
|
- An ellipse has foci at F1(9, 20) and F2(49,55) in the xy-plane and is ...
Text Solution
|
- The maximum distance of the centre of the ellipse x^(2)/16+y^(2)/9=1 f...
Text Solution
|
- P(1) and P(2) are the lengths of the perpendicular from the foci on th...
Text Solution
|
- From the focus (-5,0) of the ellipse (x^(2))/(45)+(y^(2))/(20) =1, a r...
Text Solution
|
- Let 5x-3y=8sqrt2 be normal at P(5/(sqrt(2)),3/(sqrt(2))) to an ellipse...
Text Solution
|
- If the normals at alpha, beta,gamma and delta on an ellipse are concur...
Text Solution
|
- Prove that the chords of contact of pairs of perpendicular tangents to...
Text Solution
|
- Consider an ellipse x^2/25+y^2/9=1 with centre c and a point P on it ...
Text Solution
|