Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.13|4 VideosCIRCLE
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.14|4 VideosCIRCLE
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.11|4 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 VideosCIRCLES
CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-CIRCLE -CONCEPT APPLICATION EXERCISE 4.12
- Number of integral values of lambda for which x^2 + y^2 + 7x + (1-lamb...
Text Solution
|
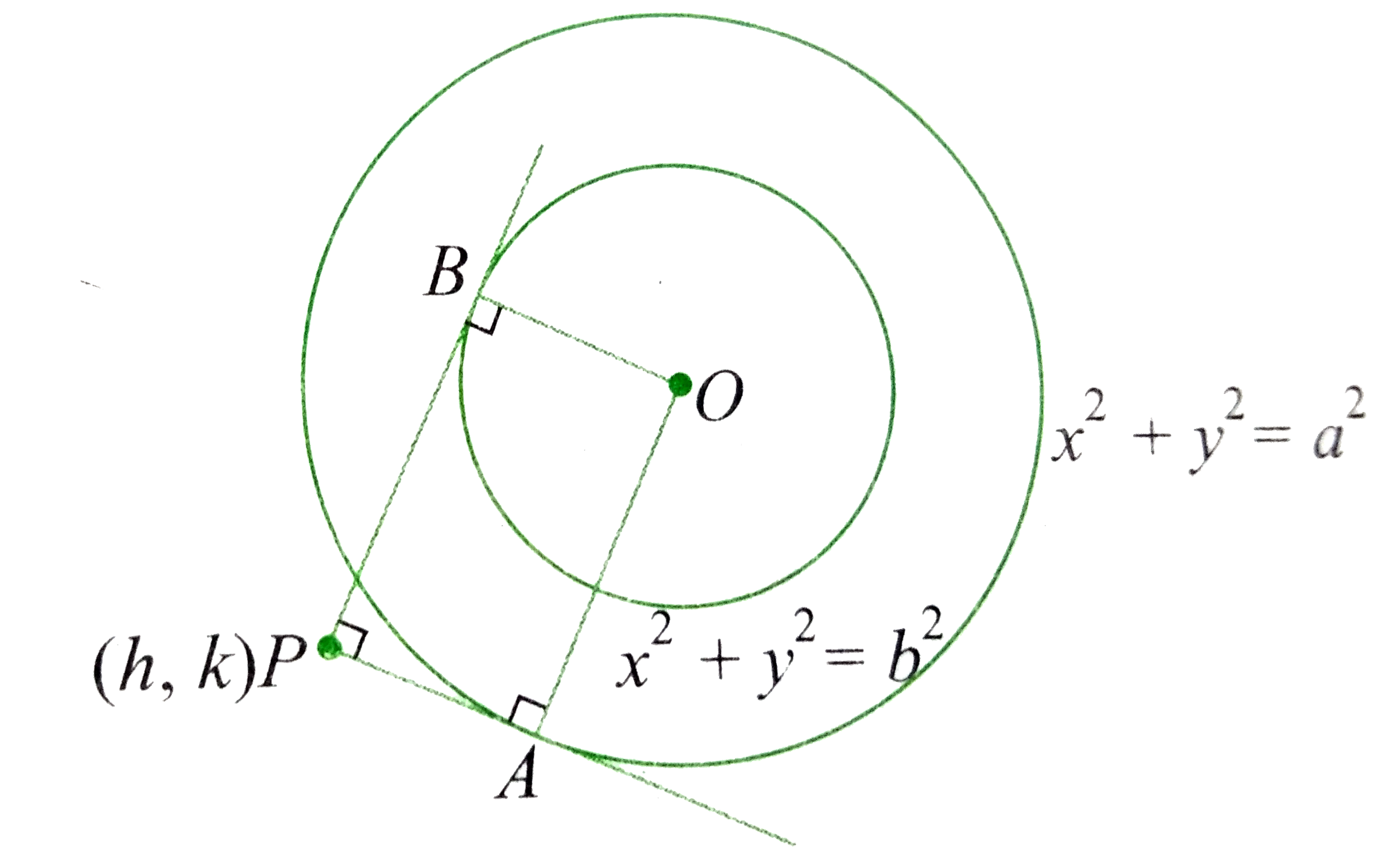
- A tangent is drawn to each of the circles x^2+y^2=a^2 and x^2+y^2=b^2d...
Text Solution
|
- An infinite number of tangents can be drawn from (1,2) to the circle x...
Text Solution
|
- Consider four circles (x+-1)^2+(y+-1)^2=1 . Find the equation of the s...
Text Solution
|