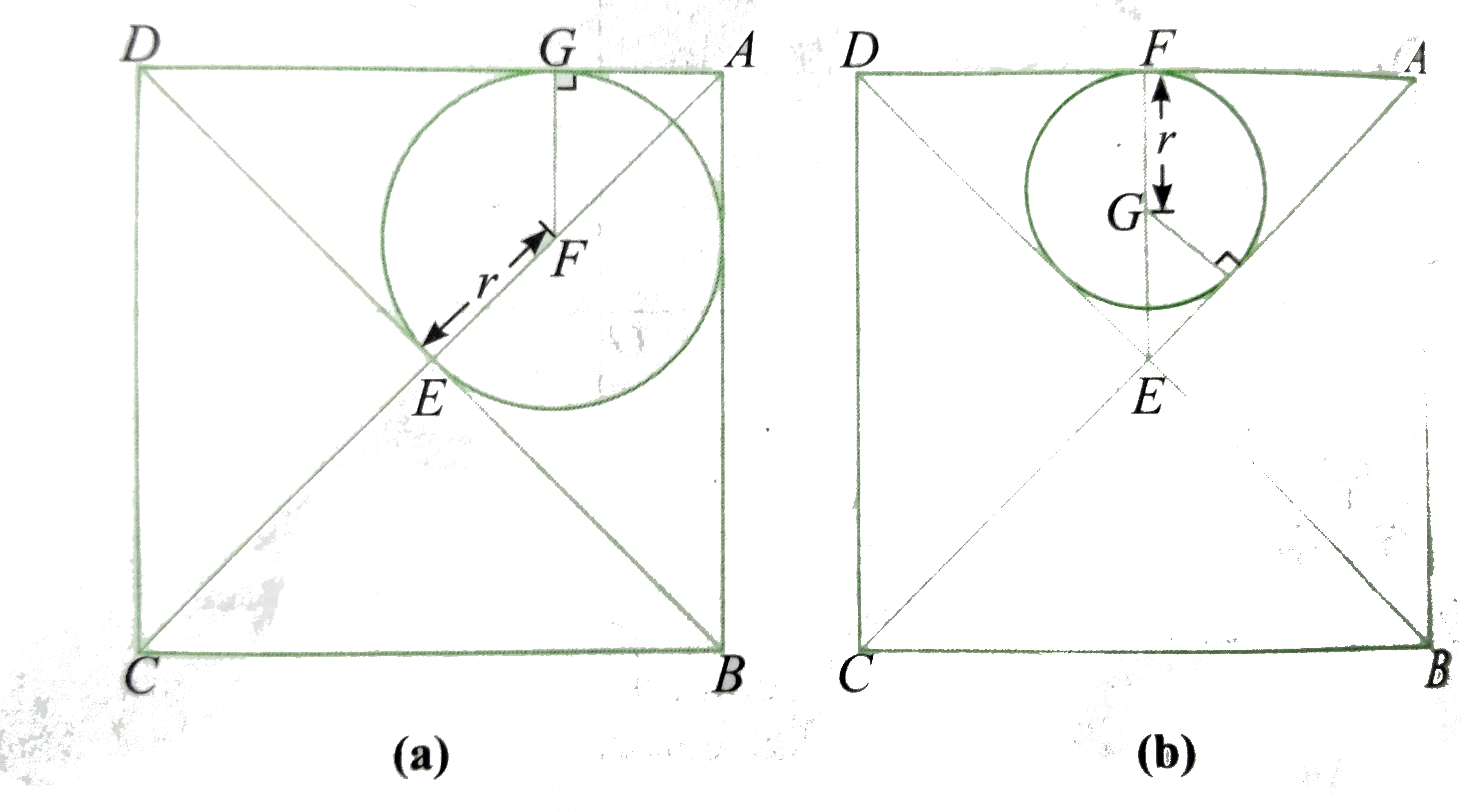
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
CENGAGE ENGLISH|Exercise For Problems|43 VideosCIRCLE
CENGAGE ENGLISH|Exercise NUMERICAL VALUE TYPE|21 VideosCIRCLE
CENGAGE ENGLISH|Exercise Multiple Correct Anser Type|29 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 VideosCIRCLES
CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos
Similar Questions
Explore conceptually related problems