A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
CENGAGE ENGLISH|Exercise NUMERICAL VALUE TYPE|21 VideosCIRCLE
CENGAGE ENGLISH|Exercise ARCHIVES (JEE MAIN)|1 VideosCIRCLE
CENGAGE ENGLISH|Exercise Linked Comprehension Type (For Problem 1-3)|3 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 VideosCIRCLES
CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-CIRCLE -For Problems
- Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such t...
Text Solution
|
- Given two circles intersecting orthogonally having the length of commo...
Text Solution
|
- Given two circles intersecting orthogonally having the length of commo...
Text Solution
|
- Given two circles intersecting orthogonally having the length of commo...
Text Solution
|
- In the given figure, there are two circles with centers A and B. The c...
Text Solution
|
- In the given figure, there are two circles with centers A and B. The c...
Text Solution
|
- In the given figure, there are two circles with centers A and B. The c...
Text Solution
|
- Let the circles S(1)-=x^(2)+y^(2)+4y-1=0 S(2)-= x^(2)+y^(2)+6x+y+8...
Text Solution
|
- Let each of the circles S(1)-=x^(2)+y^(2)+4y-1=0 S(1)-= x^(2)+y^(2...
Text Solution
|
- Let each of the circles S(1)-=x^(2)+y^(2)+4y-1=0 S(1)-= x^(2)+y^(2...
Text Solution
|
- The line x+2y+a=0 intersects the circle x^(2)+y^(2)-4=0 at two distin...
Text Solution
|
- The line x + 2y = a intersects the circle x^2 + y^2 = 4 at two distinc...
Text Solution
|
- Let A,B, and C be three sets such that A={(x,y)|(x)/(cos theta)=(y)/...
Text Solution
|
- Let A,B, and C be three sets such that A={(x,y)|(x)/(cos theta)=(y)/...
Text Solution
|
- Consider the family of circles x^(2)+y^(2)-2x-2ay-8=0 passing through...
Text Solution
|
- Consider the family of circles x^(2)+y^(2)-2x-2ay-8=0 passing through...
Text Solution
|
- Consider the family of circles x^(2)+y^(2)-2x-2ay-8=0 passing through...
Text Solution
|
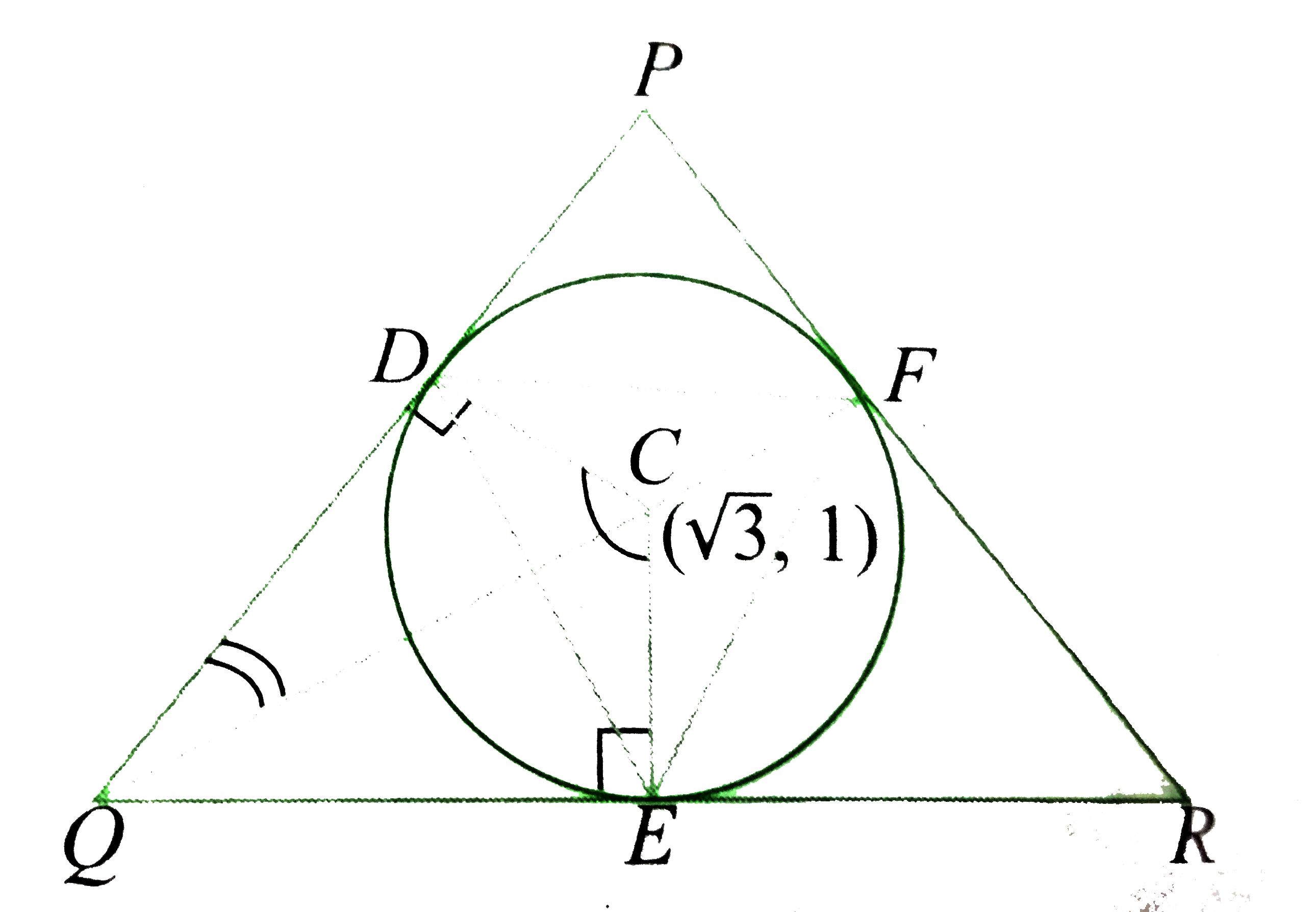
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|
- A circle C of radius 1 is inscribed in an equilateral triangle PQR. Th...
Text Solution
|