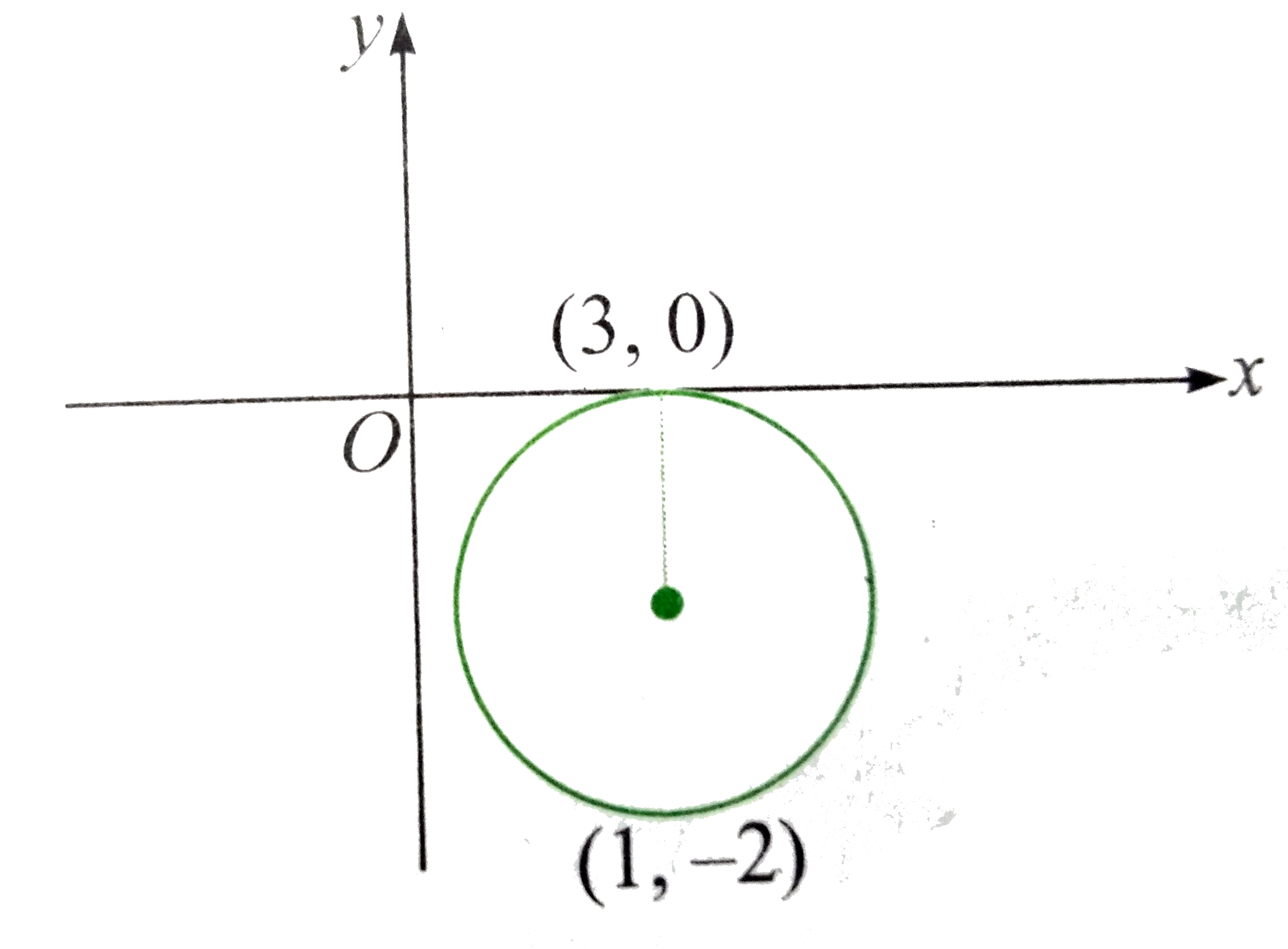A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
CENGAGE ENGLISH|Exercise JEE ADVANCED (Single Correct Answer Type)|3 VideosCIRCLE
CENGAGE ENGLISH|Exercise LINKED COMPREHENSION TYPE (For problem 1 and 2)|2 VideosCIRCLE
CENGAGE ENGLISH|Exercise ARCHIVES (JEE MAIN)|1 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 VideosCIRCLES
CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-CIRCLE -Single Correct Answer Type
- Three distinct points A, B and C are given in the 2aedimensional coord...
Text Solution
|
- If the circle x^2+y^2-4x-8y-5=0 intersects the line 3x-4y=m at two dis...
Text Solution
|
- The two circles x^2+y^2=ax and x^2+y^2=c^2(c > 0) touch each other if ...
Text Solution
|
- The length of the diameter of the circle which touches the x-axis at t...
Text Solution
|
- The circle passing through the point ( -1,0) and touching the y-axis ...
Text Solution
|
- Let C be the circle with centre at (1, 1) and radius = 1. If T is t...
Text Solution
|
- Find the number of common tangents of the circles x^2+y^2-2x-6y+9=0 an...
Text Solution
|
- The centres of those circles which touch the circle, x^2+y^2-8x-8y-4=0...
Text Solution
|
- If one of the diameters of the circle, given by the equation, x^2+y^2-...
Text Solution
|