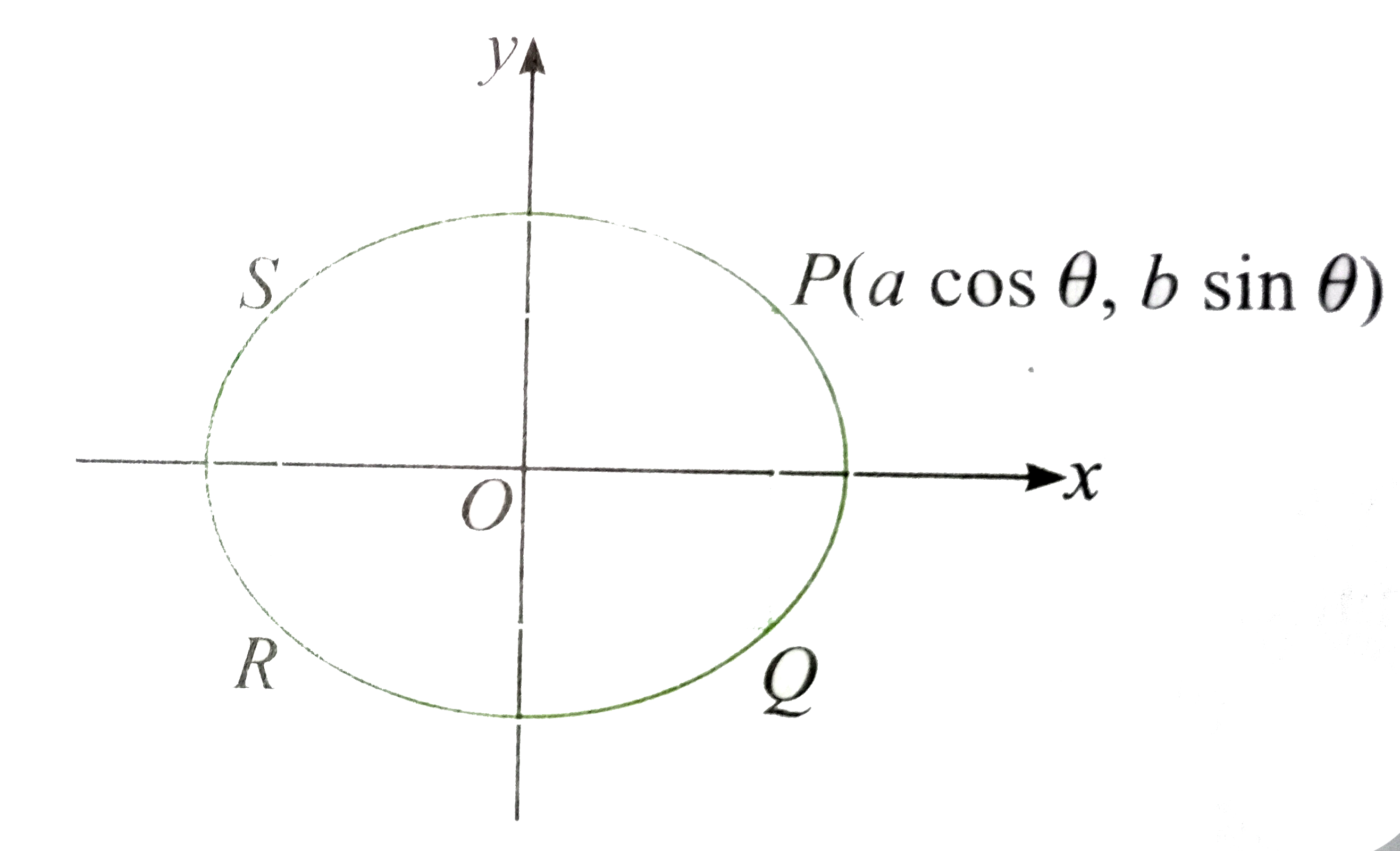
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the area of the greatest rectangle that can be inscribed in an...
Text Solution
|
- Find the area of the greatest rectangle that can be inscribed in an el...
Text Solution
|
- Area of the greatest rectangle that can be inscribed in the ellipse (x...
Text Solution
|
- Find the area of the greatest rectangle that can be inscribed in an el...
Text Solution
|
- Area of the greatest rectangle inscribed in the ellipse x^(2)/a^(2) ...
Text Solution
|
- Area ( in square unit) of the greatest rectangle that can be inscribe...
Text Solution
|
- 2.The area of the greatest rectangle that can be inscribed in the elli...
Text Solution
|
- Area of the greatest rectangle that can be inscribed in the ellipse (x...
Text Solution
|
- Find the area of the greatest rectangle that can be inscribed in an el...
Text Solution
|