Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
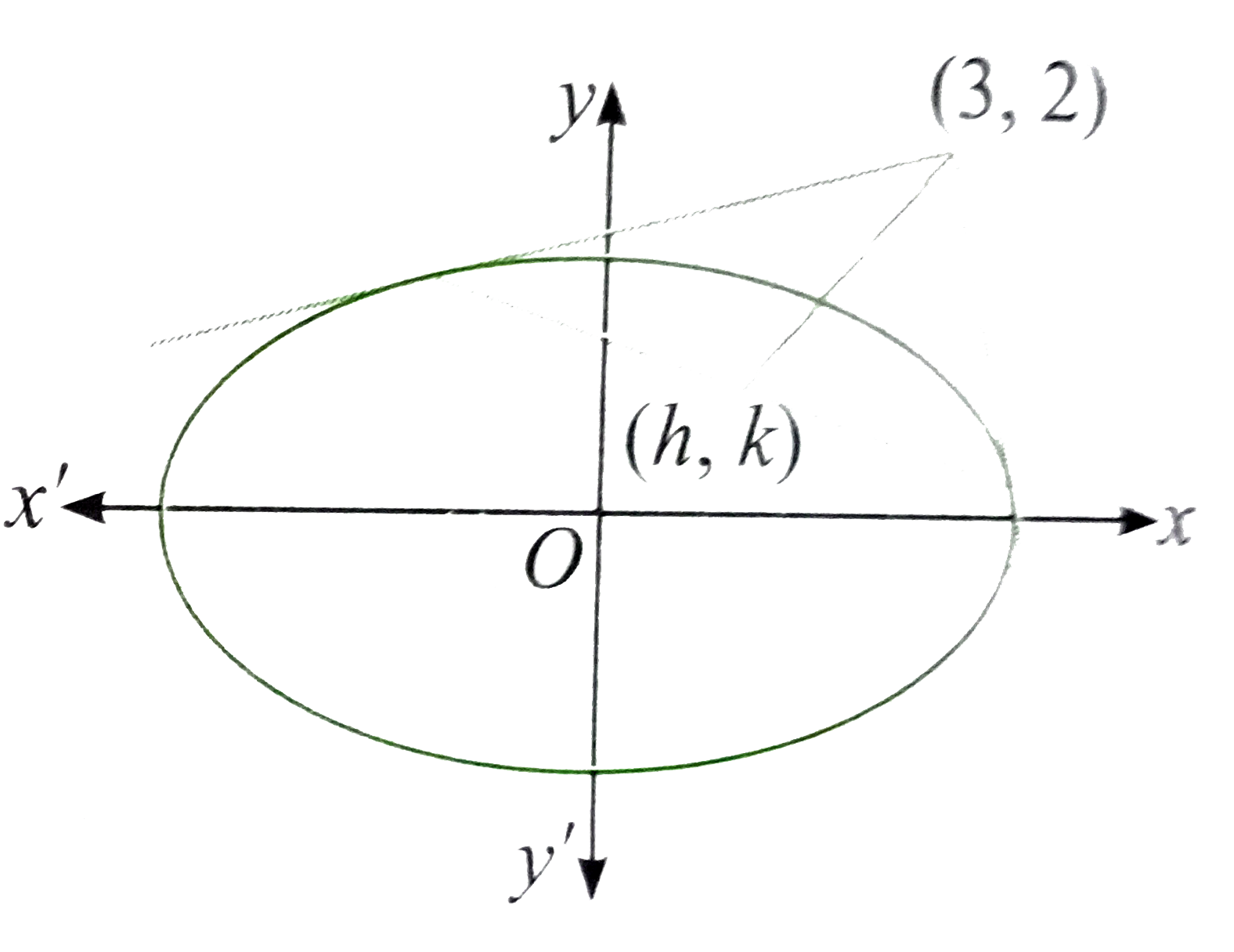
- Tangent are drawn from the point (3, 2) to the ellipse x^2+4y^2=9 ....
Text Solution
|
- Tangent are drawn from the point (3, 2) to the ellipse x^2+4y^2=9 ....
Text Solution
|
- Find the equation to the chord of contact of the tangents drawn from a...
Text Solution
|
- Find the area of the quadrilateral formed by common tangents drawn fro...
Text Solution
|
- Let from a point A (h,k) chord of contacts are drawn to the ellipse x^...
Text Solution
|
- If x= 9 is a chord of contact of the hyperbola x^(2) -y^(2) =9, then ...
Text Solution
|
- If x=9 is a chord of contact of the hyperbola x^(2)-y^(2)=9, then the ...
Text Solution
|
- Let form a point A(h, k) chords of contact are drawn to the ellipse x^...
Text Solution
|
- Find the equation of the chord of contact of the point (3,1) to the el...
Text Solution
|