Home
Class 12
MATHS
Tangents P Qa n dP R are drawn at the...

Tangents `P Qa n dP R` are drawn at the extremities of the chord of the ellipse `(x^2)/(16)+(y^2)/9=1` , which get bisected at point `P(1,1)dot` Then find the point of intersection of the tangents.

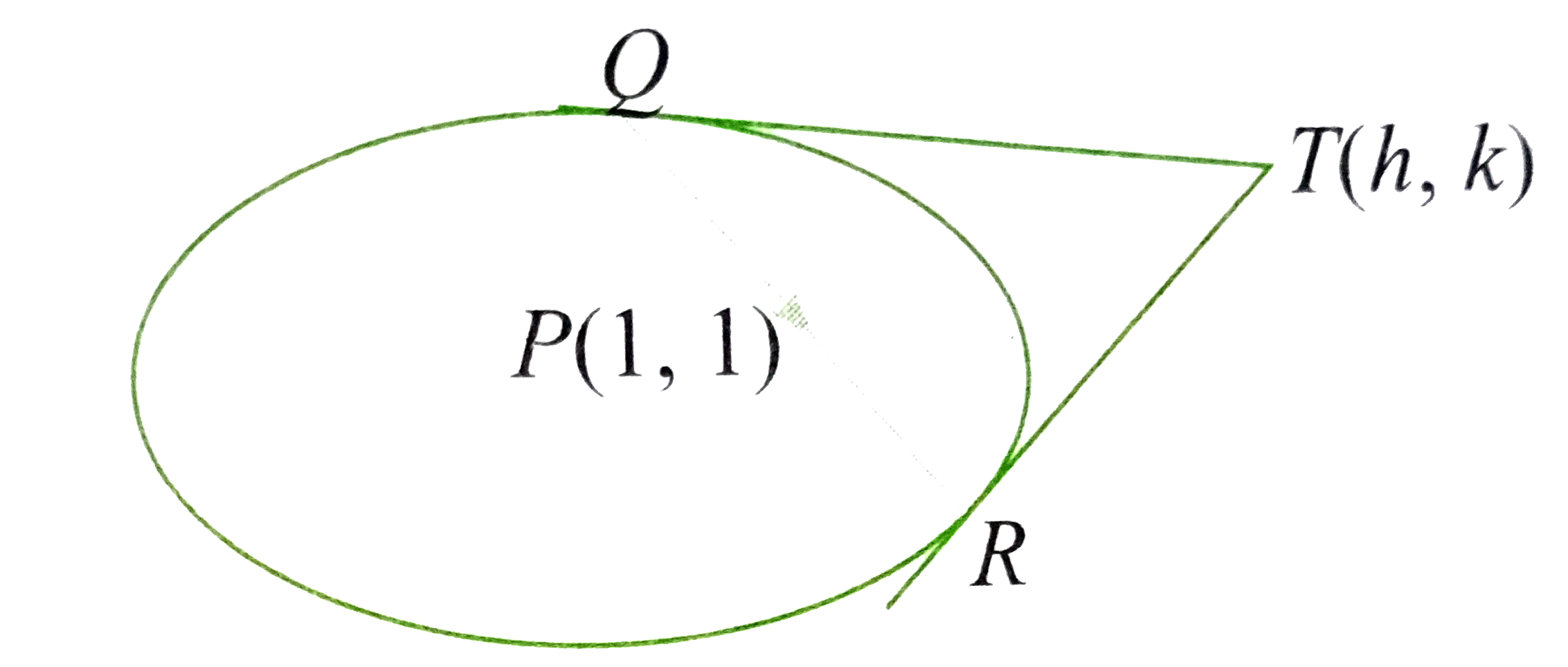
Text Solution

Verified by Experts

The correct Answer is:
`((144)/(25),(144)/(25))`

Eqution of chord having midpoint P(1,1) is
`(1*x)/(16)+(1*y)/(9)-1=(1)/(16)+(1)/(9)-1`
or `(x)/(16)+(y)/(9)=(25)/(144)`
`or 9x+16y=25" (1)`
Also, line QR is chord of contact w.r.t. point (h,k).
It equations is
`(hx)/(16)+(ky)/(9)=1`
or `9hx+16ky=144 " "(2)`
Equatiosn (1) and (2) represent the same stragith line.
`:. (9h)/(9)=(16k)/(16)=(144)/(25)`
`rArr(h,k)-=((144)/(25),(144)/(25))`
Promotional Banner

Similar Questions

Explore conceptually related problems

The equation of the chord of the ellipse 2x^2+ 5y^2 =20 which is bisected at the point (2, 1) is

The equation of the chord of the ellipse 2x^2+ 5y^2 =20 which is bisected at the point (2, 1) is

Find the equation of the tangents of the ellipse (x ^(2)) /(16) + (y ^(2))/(9) =1, which make equal intercepts on the axes.

Find the equations of the tangent drawn to the ellipse (x^(2))/(3) + y^(2) =1 from the point (2, -1 )

If PQ is the focal chord of the parabola y^(2)=-x and P is (-4, 2) , then the ordinate of the point of intersection of the tangents at P and Q is

If the tangents to the parabola y^2=4a x intersect the hyperbola (x^2)/(a^2)-(y^2)/(b^2)=1 at Aa n dB , then find the locus of the point of intersection of the tangents at Aa n dBdot

Tangents are drawn at the ends of any focal chord of the parabola y^(2)=16x . Then which of the following statements about the point of intersection of tangents is true.

Tangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/4=1 touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is

The locus of the point of intersection of tangents to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 which meet at right , is

Statement-1: The tangents at the extremities of a focal chord of the parabola y^(2)=4ax intersect on the line x + a = 0. Statement-2: The locus of the point of intersection of perpendicular tangents to the parabola is its directrix