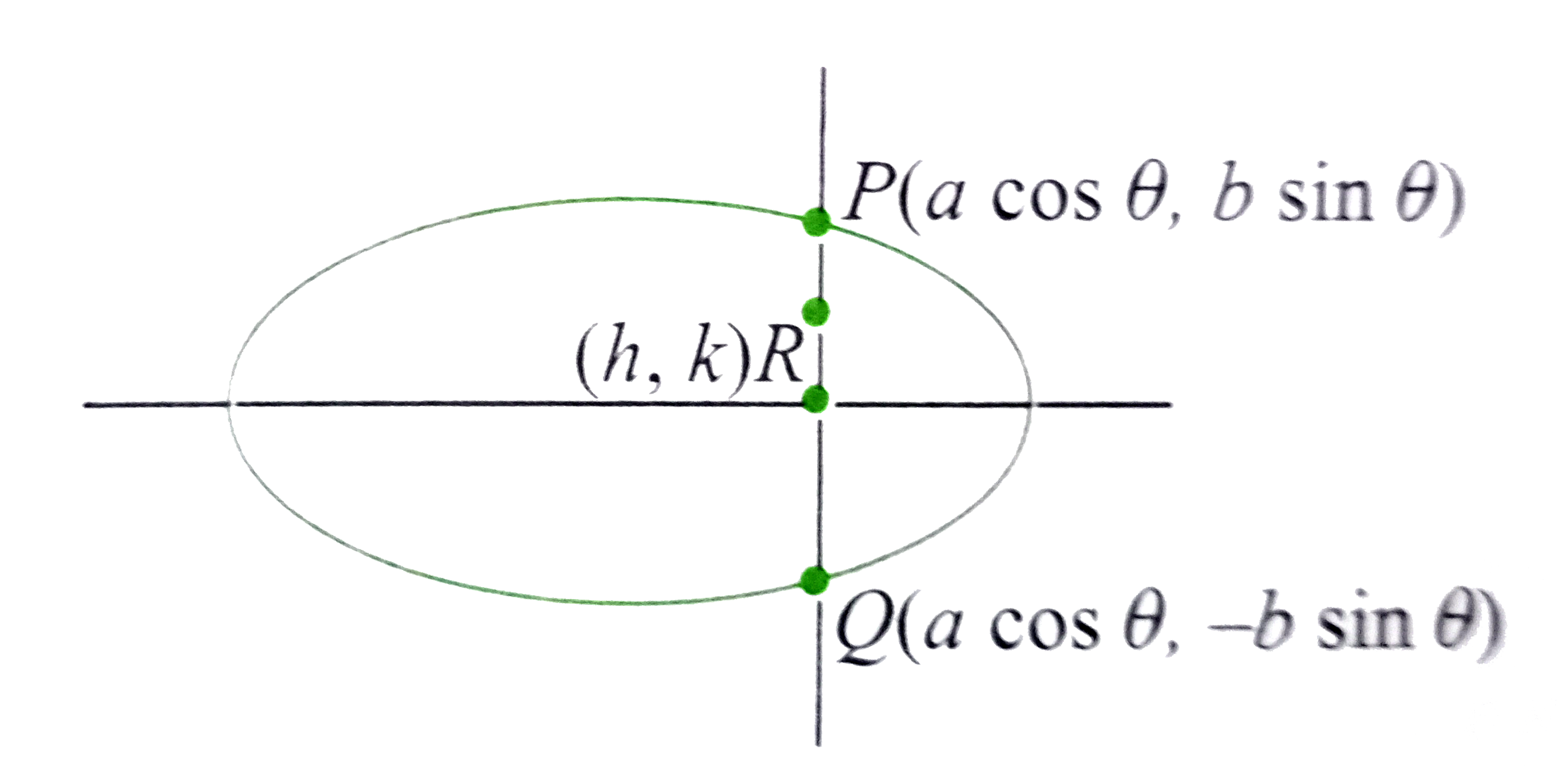
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The locus of the point which divides the double ordinates of the ell...
Text Solution
|
- The locus of the point which divides the double ordinates of the el...
Text Solution
|
- A=(2,-1) locus of B is x^(2)+y^(2)=25. If P divides AB in the ratio 1:...
Text Solution
|
- the locus of the point of intersection of tangents to the ellipse...
Text Solution
|
- The locus of a point which divides the join of A(-1, 1) and a variable...
Text Solution
|
- The locus of the point of intersection of the perpendicular tangents t...
Text Solution
|
- PQ is any double ordinate of the ellipse (x^(2))/(a^(2))+(y^(2))/(b...
Text Solution
|
- A is a point on the circle x^(2)+y^(2)=36. Find the locus of the point...
Text Solution
|
- P is any point on the auxililary circle of the ellipse (x^(2))/(a^(2))...
Text Solution
|