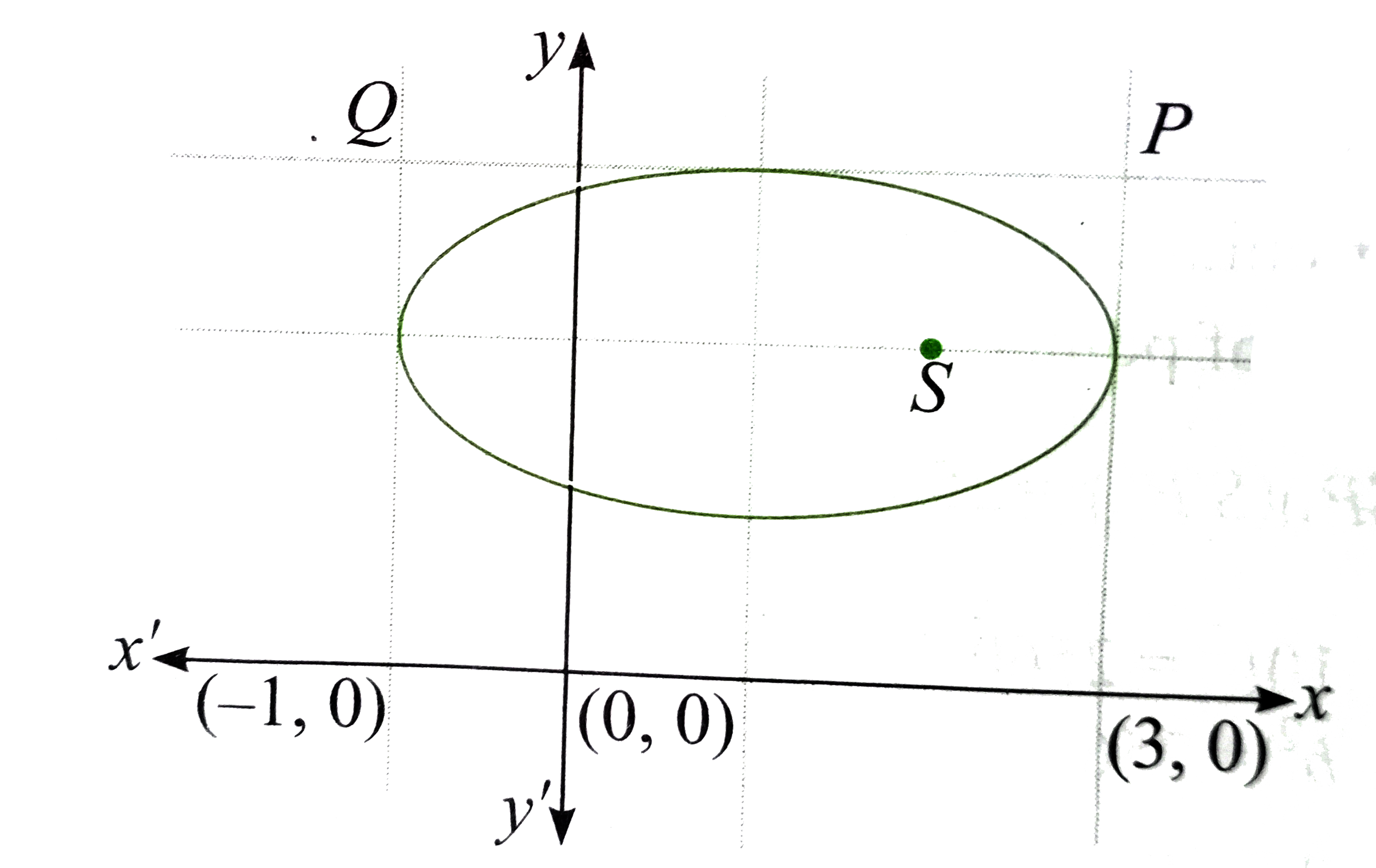
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which of the following is/are true about the ellipse x^2+4y^2-2x-16 y+...
Text Solution
|
- Statement 1 : If the line x+y=3 is a tangent to an ellipse with focie ...
Text Solution
|
- Which of the following is/are true about the ellipse x^2+4y^2-2x-16 y+...
Text Solution
|
- Let the foci of the ellipse (x^(2))/(9) + y^(2) = 1 subtend a right ...
Text Solution
|
- Statement 1 The tangent and normal at any point P on a ellipse bisect ...
Text Solution
|
- Find the length of the latus rectum of the ellipse 5x^(2) + 3y^(2) = ...
Text Solution
|
- The vertices of the triangle ABC are A(0, 0), B(3, 0) and C(3, 4), whe...
Text Solution
|
- " Eccentricity of ellipse "(x^(2))/(a^(2))+(y^(2))/(b^(2))=1" such tha...
Text Solution
|
- A tangent to the ellipse x^2+4y^2=4 meets the ellipse x^2+2y^2=6 at P ...
Text Solution
|