A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
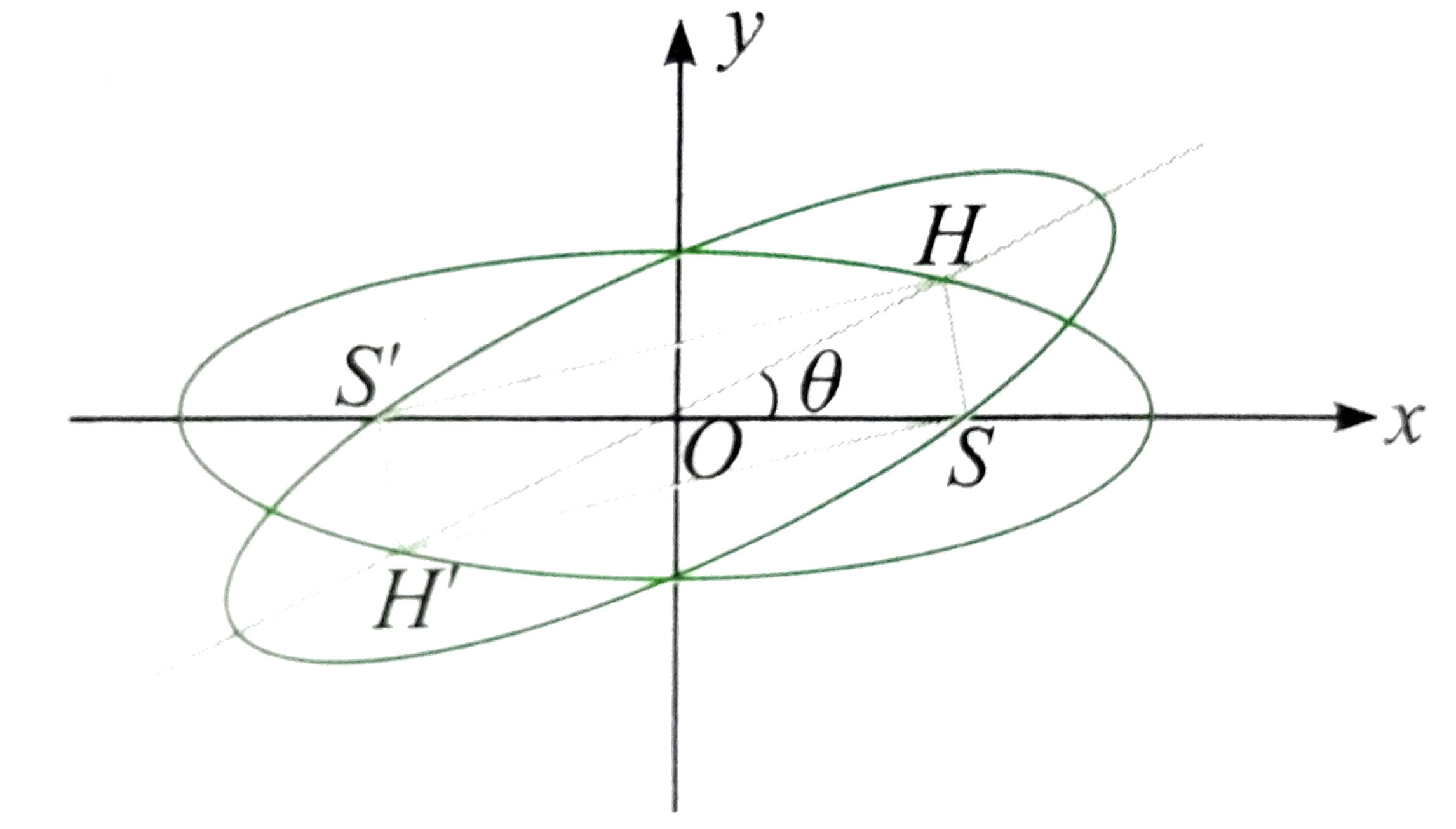
- Two concentric ellipses are such that the foci of one are on the other...
Text Solution
|
- If PSQ+ PHR be two chords of an ellipse through its foci S and H, then...
Text Solution
|
- If PSQ + PHR be two chords of an ellipse through its foci S and H, the...
Text Solution
|
- Two concentric ellipses are such that the foci of one are on the other...
Text Solution
|
- A variable point P on the ellipse of eccentricity e is joined to the f...
Text Solution
|
- If two concentric elipse be such that the foci of one be on the and if...
Text Solution
|
- Two concentric ellipse be such that the foci of one be on the other an...
Text Solution
|
- Find the length of the latus rectum of the ellipse 5x^(2) + 3y^(2) = ...
Text Solution
|
- If the angle between the lines joining the Foci to an extremity of ...
Text Solution
|