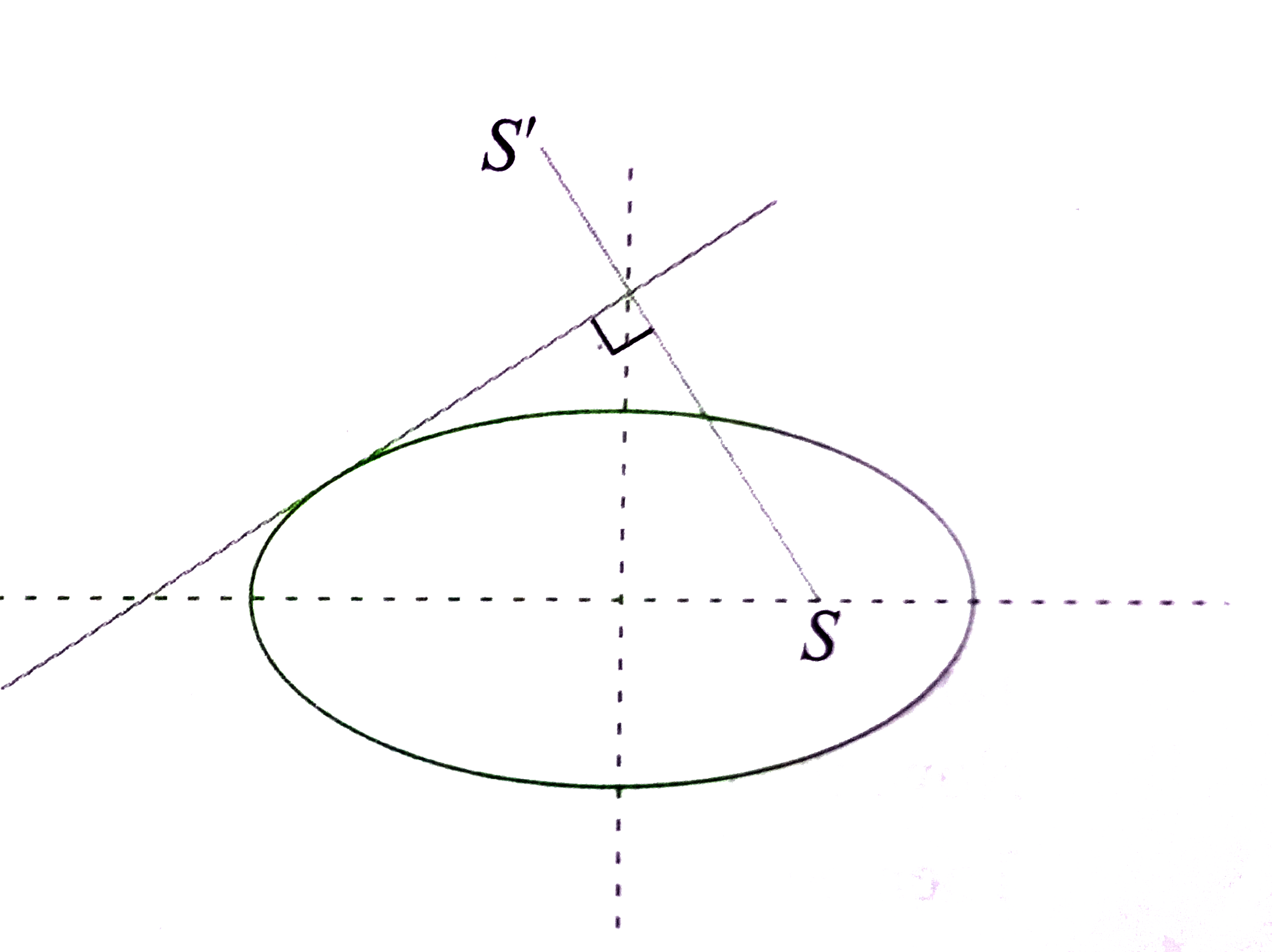
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The locus of the image of the focus of the ellipse (x^2)/(25)+(y^2)/9-...
Text Solution
|
- The locus of the image of the focus of the ellipse (x^2)/(25)+(y^2)/9=...
Text Solution
|
- The locus of the point of intersection of the tangents at the extre...
Text Solution
|
- Locus of feet of perpendicular from (5,0) to the tangents of (x^(2))/(...
Text Solution
|
- Let the foci of the ellipse (x^(2))/(9)+y^(2)=1 subtend a right angle ...
Text Solution
|
- The locus of poles of tangents to the ellipse (x^(2))/(a^(2))+(y...
Text Solution
|
- The locus of the poles of tangents to the director circle of the ellip...
Text Solution
|
- The locus pf the image of the focus of the ellipse x^(2)/25+y^(2)/9=1,...
Text Solution
|
- The minimum length of intercept on any tangent to the ellipse (x^(2))/...
Text Solution
|