A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
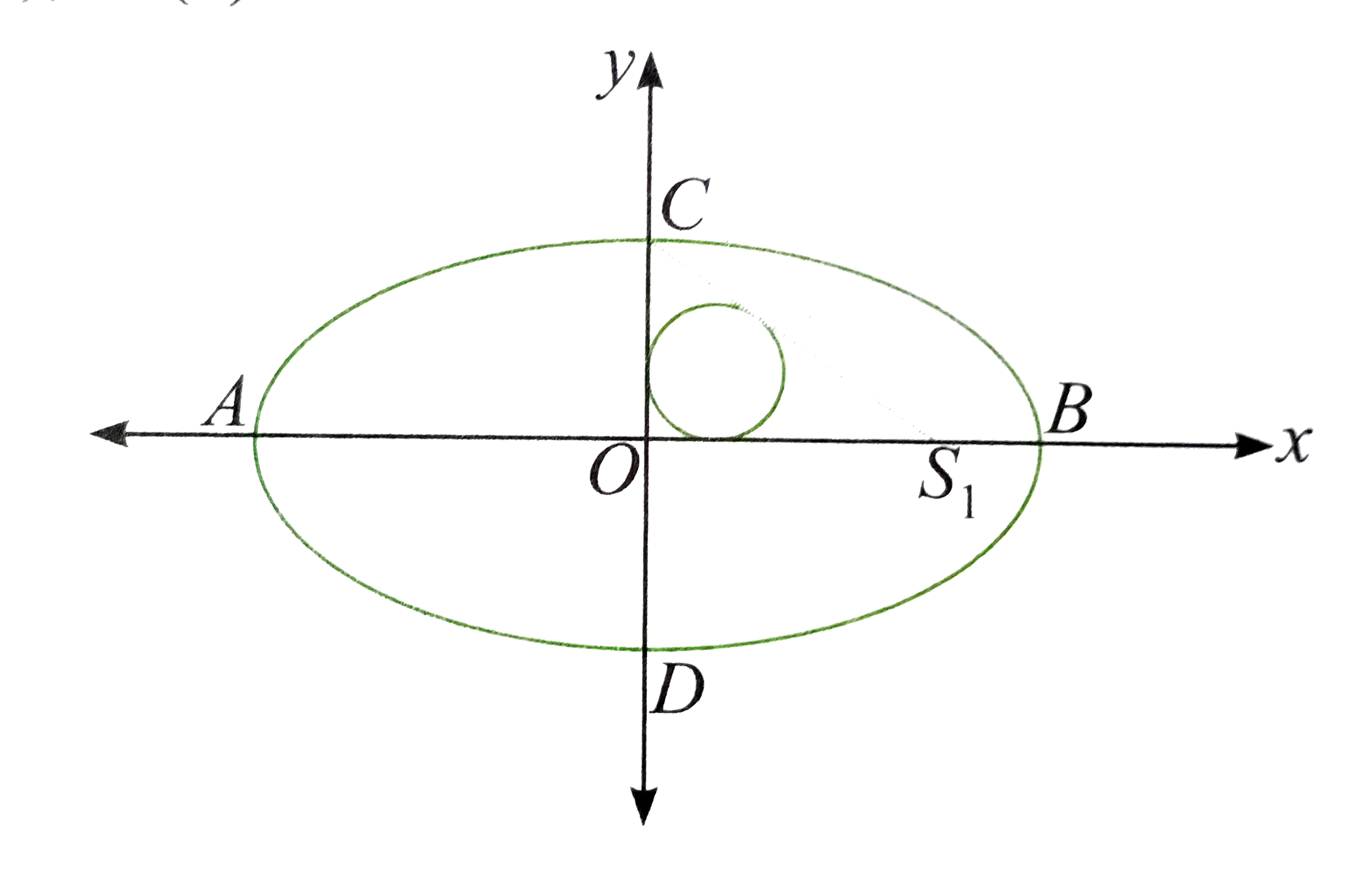
- Consider an ellipse E:x^(2)/a^(2)+y^(2)/b^(2)=1, centered at point 'O'...
Text Solution
|
- Consider an ellipse E ,(x^2)/(a^2)+(y^2)/(b^2)=1 , centered at point O...
Text Solution
|
- Point 'O' is the centre of the ellipse with major axis AB & minor ...
Text Solution
|
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- Consider an ellipse E:x^(2)/a^(2)+y^(2)/b^(2)=1, centered at point 'O'...
Text Solution
|
- Consider an ellipse E ,(x^2)/(a^2)+(y^2)/(b^2)=1 , centered at point O...
Text Solution
|
- एक दीर्घवृत्त (E)(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, जिसका केन्द्र 'O' ...
Text Solution
|