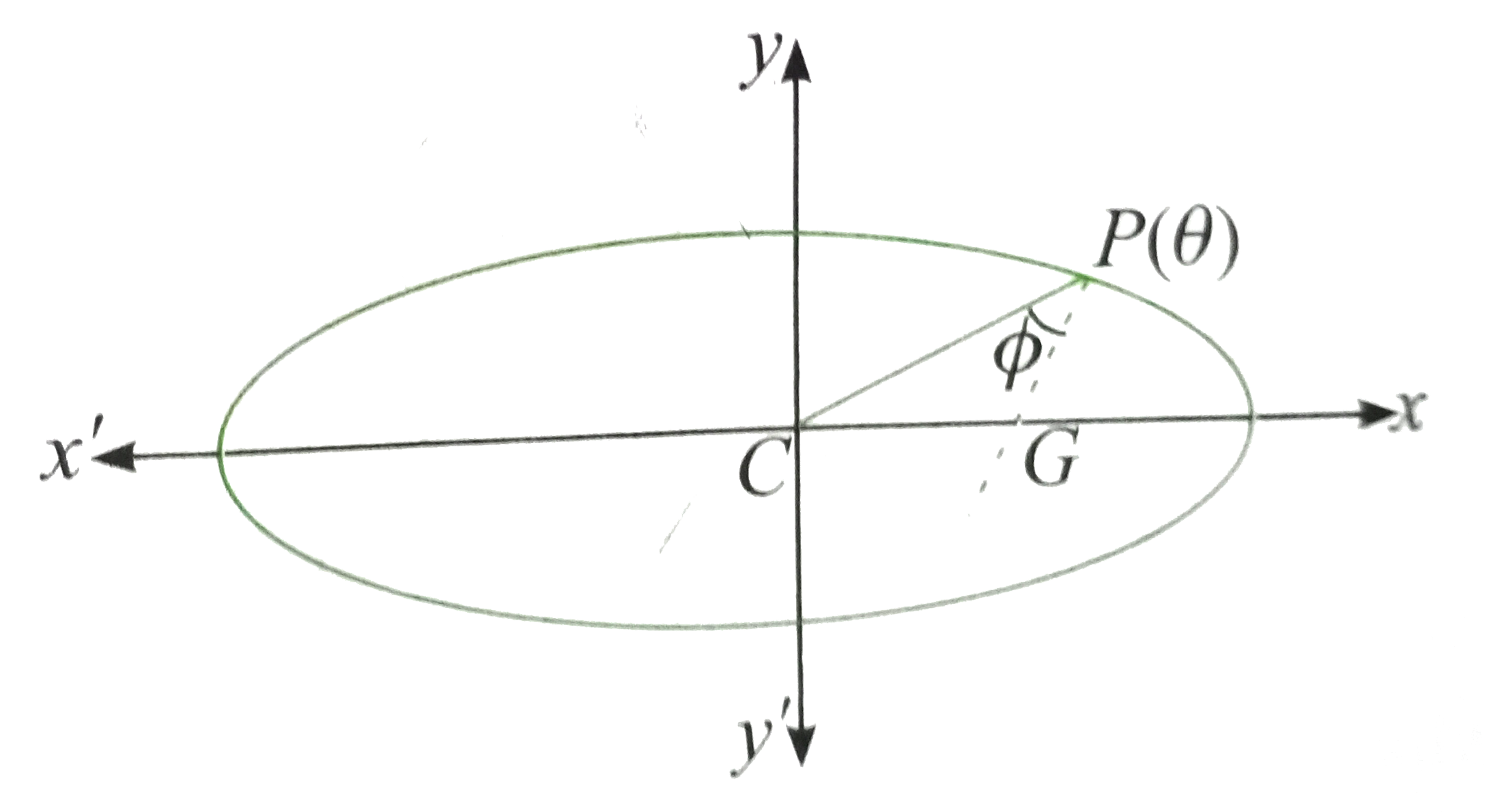
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider the ellipse whose major and minor axes are x-axis and y-axis,...
Text Solution
|
- Consider the ellipse whose major and minor axes are x-axis and y-axis,...
Text Solution
|
- An ellipse hase semi-major of length 2 and semi-minor axis of length 1...
Text Solution
|
- If the length of the major axis of an ellipse is 17/8 times the length...
Text Solution
|
- If the length of the major axis of an ellipse is three times the leng...
Text Solution
|
- The lengths of major and minor axis of an ellipse are 10 and 8 respect...
Text Solution
|
- The equation of the ellipse with it's major axis is x-axis, minor axis...
Text Solution
|
- The eccentricity of the ellipse whose major axis is double the minor a...
Text Solution
|
- The major axis of an ellipse is y=x and one vertex is at origin, then ...
Text Solution
|