A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
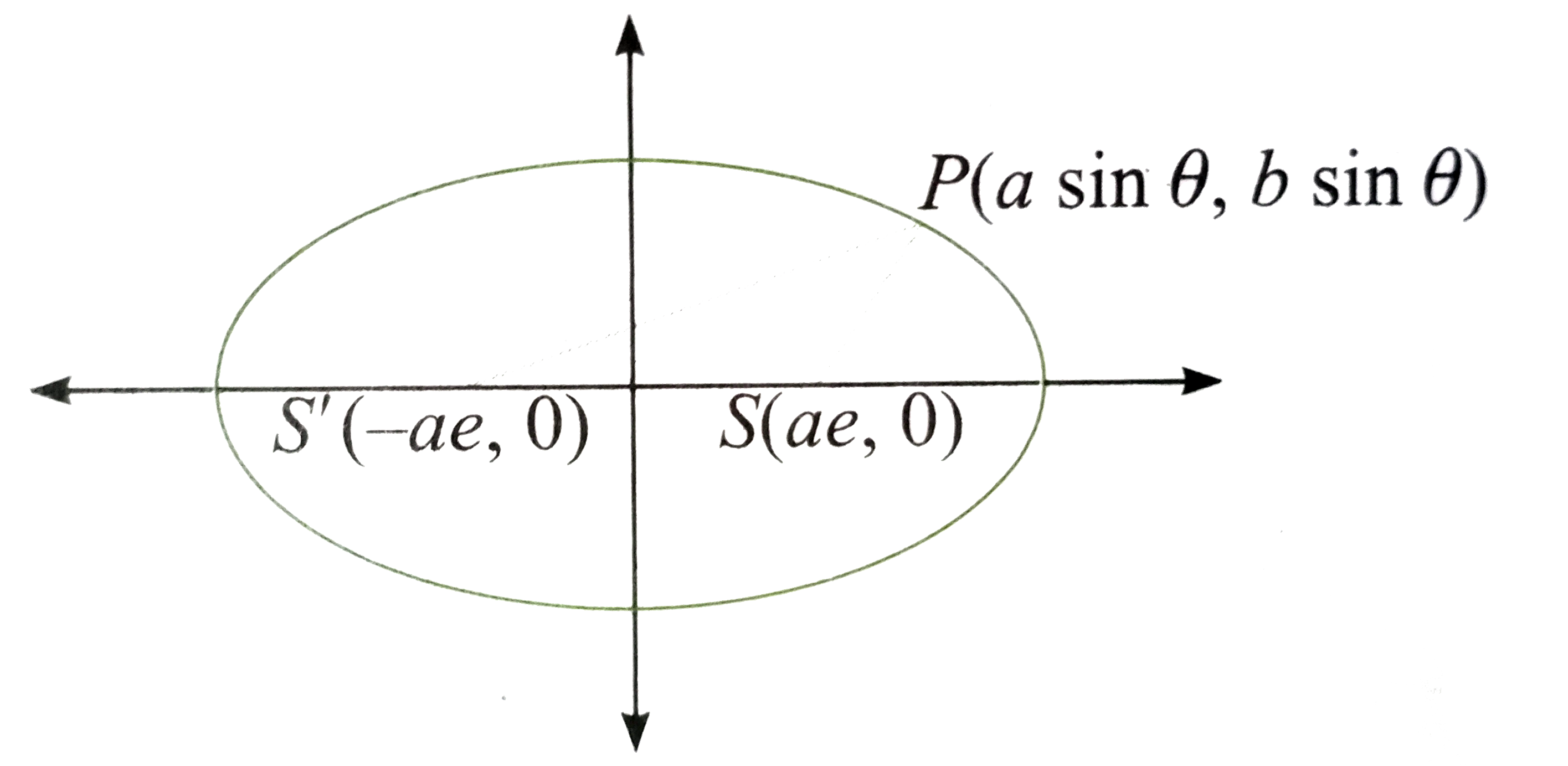
- Let S and S'' be the fociof the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- If P is a variable point on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- The locus of point of intersection of tangents to an ellipse (x^(2))/(...
Text Solution
|
- Let S and S'' be the fociof the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- Let S and S'' be the foci of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2...
Text Solution
|
- The locus of the point of intersection of tangents to the ellipse x^(2...
Text Solution
|
- Find the equation of the ellipse whose length of major axis is 4 and l...
Text Solution
|
- Locus of mid-point of the focal chord of ellipse (x^(2))/(a^(2))+(y^(...
Text Solution
|
- Let S and S'' be the fociof the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|