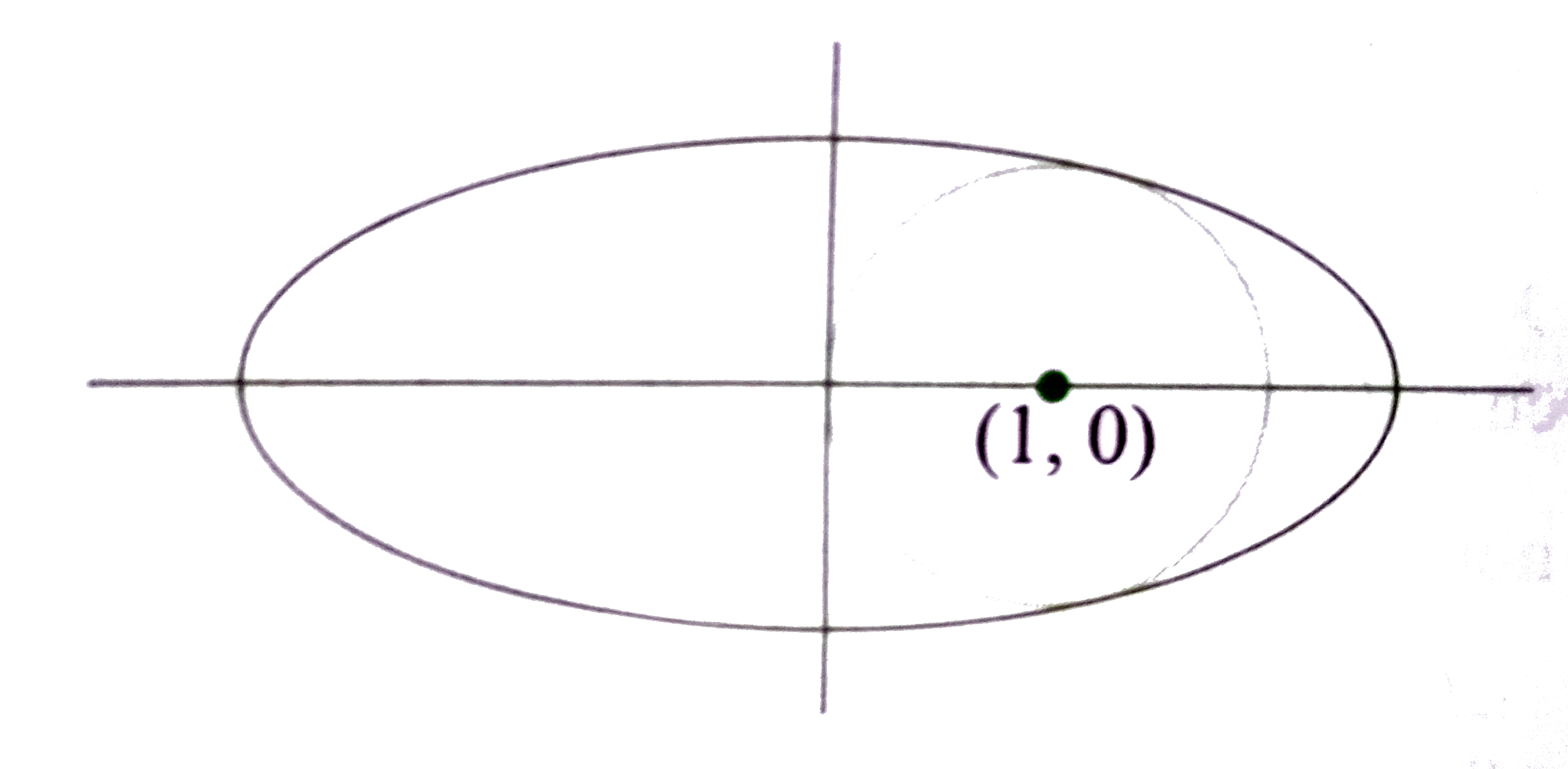
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Area bounded by the ellipse (x^2)/(4)+(y^2)/(9)=1 is equal to
Text Solution
|
- Find the area of the region bounded by the ellipse (x^2)/4+(y^2)/9=1
Text Solution
|
- Evaluate the area bounded by the ellipse (x^2)/(4)+(y^2)/(9)=1 above...
Text Solution
|
- Find the area of the region bounded by the ellipse (x^(2))/(9)+(y^(2))...
Text Solution
|
- The area bounded by the ellipse x^(2)/4 + y^(2)/25 = 1 is
Text Solution
|
- Area bounded by the ellipse (x^2)/(4)+(y^2)/(9)=1 is equal to
Text Solution
|
- Find the area of the region bounded by the ellipse (x^2)/(4)+(y^2)/(9)...
Text Solution
|
- Find the area of the region bounded by the ellipse (x ^(2))/(4) + (y ^...
Text Solution
|
- Find the area of the region bounded by the ellipse (x^(2))/(4) + (y^(2...
Text Solution
|