Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
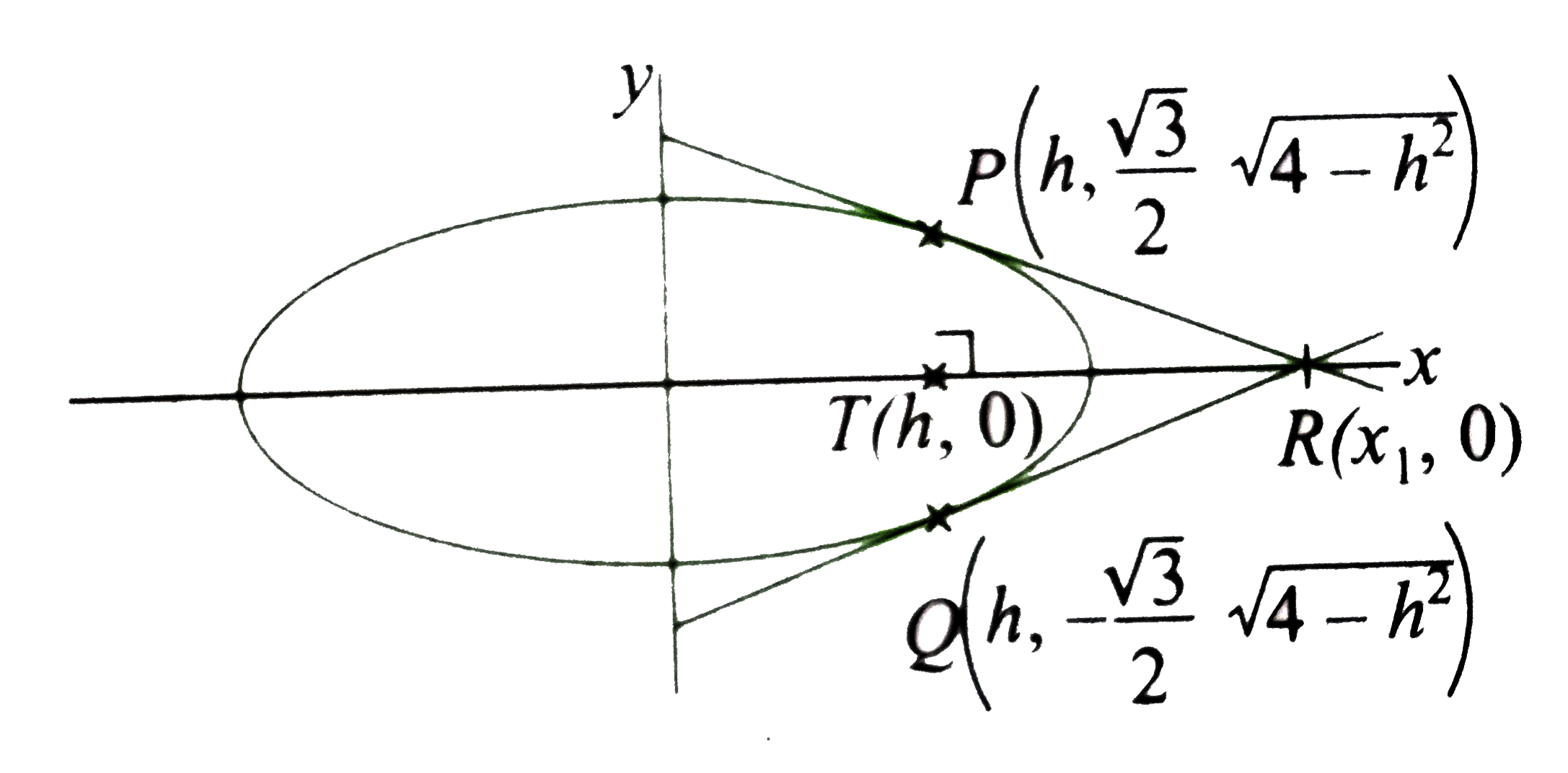
- A vertical line passing through the point (h, 0) intersects the ellips...
Text Solution
|
- A vertical line passing through the point (h,0) intersects the ellipse...
Text Solution
|
- The vertices of a triangle are (1, 2), (h, -3) and (-4, k). Find the v...
Text Solution
|
- बिन्दु (h, 0) से गुजरने वाली एक ऊर्ध्वाधर रेखा दीर्घवृत्त x^2/4+y^2/3=...
Text Solution
|
- The area of the triangle formed by the intersection of a line parallel...
Text Solution
|
- Tangents are drawn to x^2+y^2=16 from the point P(0, h)dot These tange...
Text Solution
|
- Consider the parabola y^2 = 8x. Let Delta1 be the area of the triangle...
Text Solution
|
- A vertical line passing through the point (h, 0) intersects the ellips...
Text Solution
|
- If S + O(2) rarr SO(2), Delta H = -398.5 kJ SO(2) + (1)/(2)O(2) rarr...
Text Solution
|