Text Solution
Verified by Experts
Topper's Solved these Questions
THEORY OF EQUATIONS
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 2.1|3 VideosTHEORY OF EQUATIONS
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 2.2|5 VideosTHEORY OF EQUATIONS
CENGAGE ENGLISH|Exercise ILLUSTRATION|122 VideosSTRAIGHT LINES
CENGAGE ENGLISH|Exercise ARCHIVES (NUMERICAL VALUE TYPE)|1 VideosTHREE DIMENSIONAL GEOMETRY
CENGAGE ENGLISH|Exercise All Questions|294 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-THEORY OF EQUATIONS-SOLVED EXAMPLES
- IF [x^(2) - 2x + a]=0 has no solution, then find the values of a (wher...
Text Solution
|
- If a(1) x^(3) + b(1)x^(2) + c(1)x + d(1) = 0 and a(2)x^(3) + b(2)x^(2)...
Text Solution
|
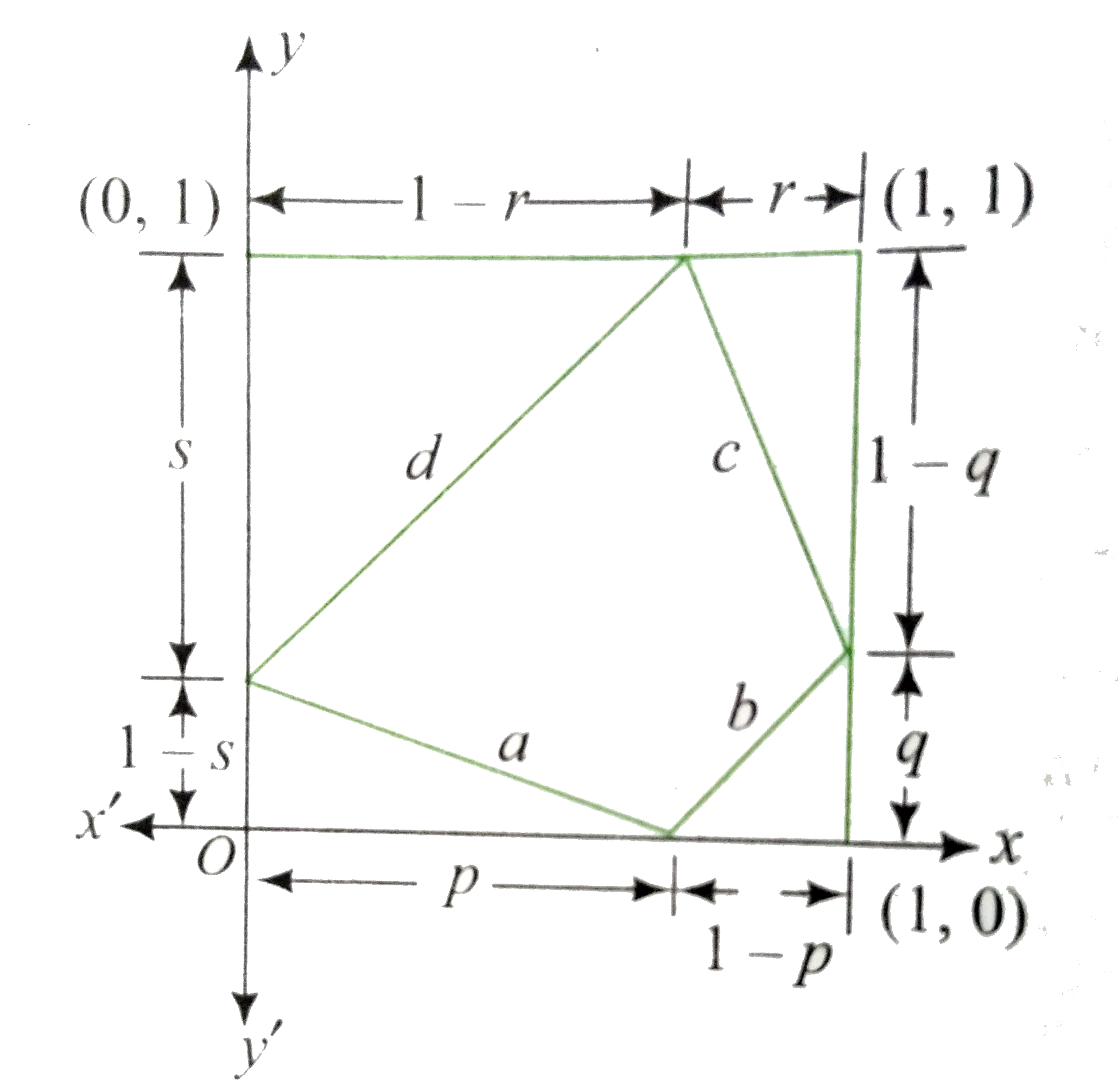
- Let S be a square of unit area. Consider any quadrilateral which has o...
Text Solution
|
- Show that the minimum value of (x+a)(x+b)//(x+c)dotw h e r ea > c ,b >...
Text Solution
|
- Let f(x),g(x),a n dh(x) be the quadratic polynomials having positive l...
Text Solution
|
- If the slope of one of the pairs of lines represented by equation a^(3...
Text Solution
|
- If f(x)=(a1x+b1)^2+(a2x+b2)^2+...+(an x+bn)^2 , then prove that (a1b1+...
Text Solution
|
- Find the values of a for which the expression (ax^2+3x-4)/(3x-4x^2+a) ...
Text Solution
|
- Let a ,ba n dc be real numbers such that a+2b+c=4 . Find the maximum v...
Text Solution
|
- If x^(4) + 2kx^(3) + x^(2) + 2kx + 1 = 0 has exactly tow distinct...
Text Solution
|
- Find the value of a for which the equation a sin(x+pi/4)=sin2x+9...
Text Solution
|
- Prove that if 2a0^2<15 a , all roots of x^5-a0x^4+3a x^3+b x^2+c x+d=0...
Text Solution
|
- Find the values ' a ' for which the function f(x)=(a+2)x^3-3a x^2+9a x...
Text Solution
|
- Find the number of points of local extrema of f(x)=3x^4-4x^3+6x^2+ax+b...
Text Solution
|