Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
HC VERMA ENGLISH-WORK AND ENERGY-Worked out Examples
- A porter lifts a suitcase weighing 20 kg from the platform and puts it...
Text Solution
|
- An elevator weighing 500 kg is to be lifted up at a constant velociy o...
Text Solution
|
- A block of mas 2.0 kg is pulled up on a smooth incline of angle 30^0 w...
Text Solution
|
- A force F=(10+0.50x) acts on a particle in the x direction, where F is...
Text Solution
|
- A body dropped from a height H reaches the ground with a speed of 1.2 ...
Text Solution
|
- A block of mass M is pulled along a horizontal surface by applying a f...
Text Solution
|
- Two identical cylindrical vessel with their bases at the same level ea...
Text Solution
|
- What minimum horizontal speed should be given to the bob of a simple p...
Text Solution
|
- A uniform chain of length l and mass m overhangs a smooth table with i...
Text Solution
|
- A block of mass m is pushed against a spring of spring constant k fixe...
Text Solution
|
- A particle is placed at the point A of a frictionless track ABC as sho...
Text Solution
|
- Figure shows a smooth curved track terminating in a smooth horizontal ...
Text Solution
|
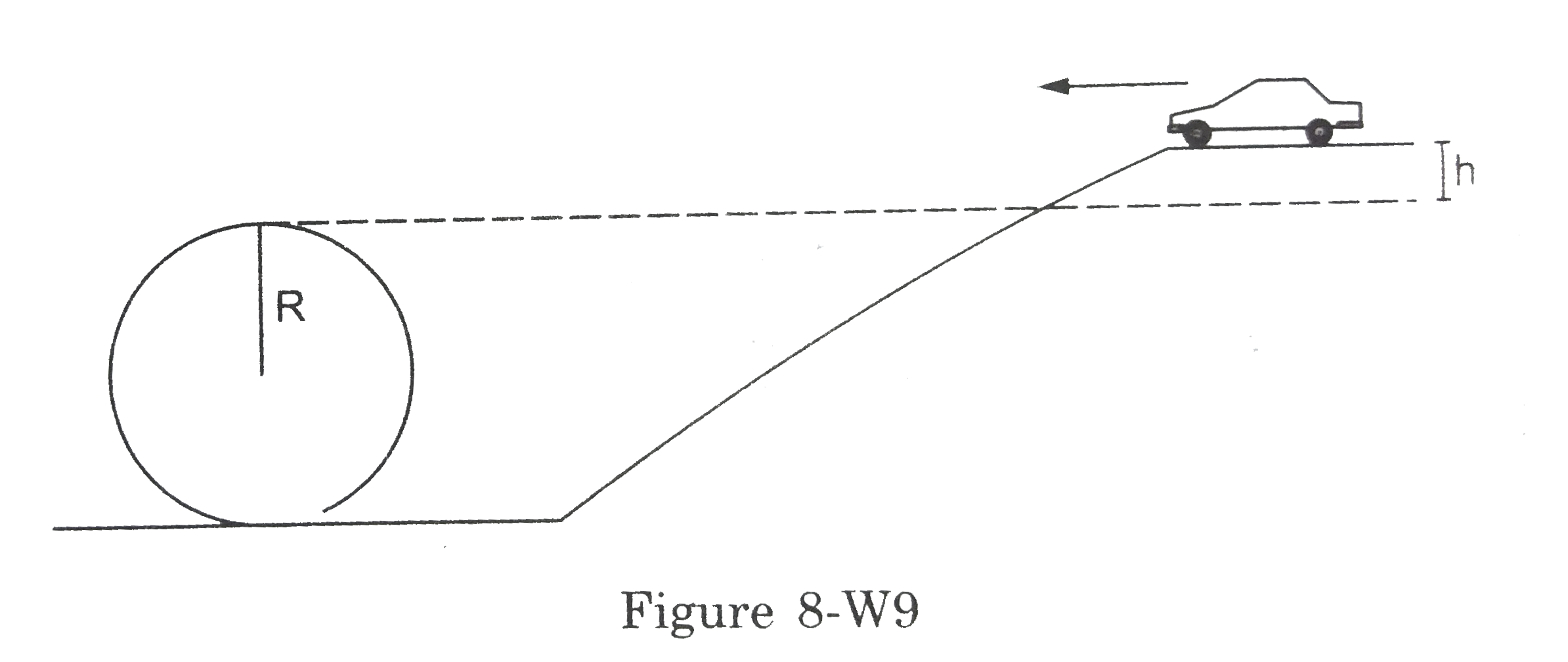
- Figure shows a loop the loop track of radius R. A car (without engine)...
Text Solution
|
- A heavy particle is suspended by a stirng of length l. The particle is...
Text Solution
|