Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
HC VERMA ENGLISH|Exercise Question for short Answer|15 VideosSIMPLE HARMONIC MOTION
HC VERMA ENGLISH|Exercise Objective-2|15 VideosROTATIONAL MECHANICS
HC VERMA ENGLISH|Exercise Questions for short Answer|21 VideosSOME MECHANICAL PROPERTIES OF MATTER
HC VERMA ENGLISH|Exercise Objective-2|7 Videos
Similar Questions
Explore conceptually related problems
HC VERMA ENGLISH-SIMPLE HARMONIC MOTION-Exercises
- A sphere of mass m and radius r radius without slipping on a rough con...
Text Solution
|
- The simple pendulum of length 40 cm is taken inside a deep mine. Assum...
Text Solution
|
- Assume that a tunnel is dug across the earth (radius = R) passing thro...
Text Solution
|
- Assume that a tunnel ils dug along a chord of the earth, at a perpendi...
Text Solution
|
- A simple pendulum of length l is suspended through the ceiling of an e...
Text Solution
|
- A simple pendulum of length 1 feet suspended from the ceiling of an el...
Text Solution
|
- A simple pendulum fixed in a car has a time period of 4 seconds when t...
Text Solution
|
- A simple pendulum of length l is suspended from the ceilling of a car ...
Text Solution
|
- The ear ring of a lady shown in figure has a 3 cm long light suspensi...
Text Solution
|
- Find the time period of small oscillations of the following system. a....
Text Solution
|
- A uniform rod of length l is suspended by end and is made to undego sm...
Text Solution
|
- A uniform disc of radius r is to be suspended through a small hole mad...
Text Solution
|
- A hollow sphere of radius 2 cm is attached to an 18 cm long thread to ...
Text Solution
|
- A closed circular wire hung on a nail in a wall undergoes small oscill...
Text Solution
|
- A uniform disc of mass m and radius r is suspended through a wire atta...
Text Solution
|
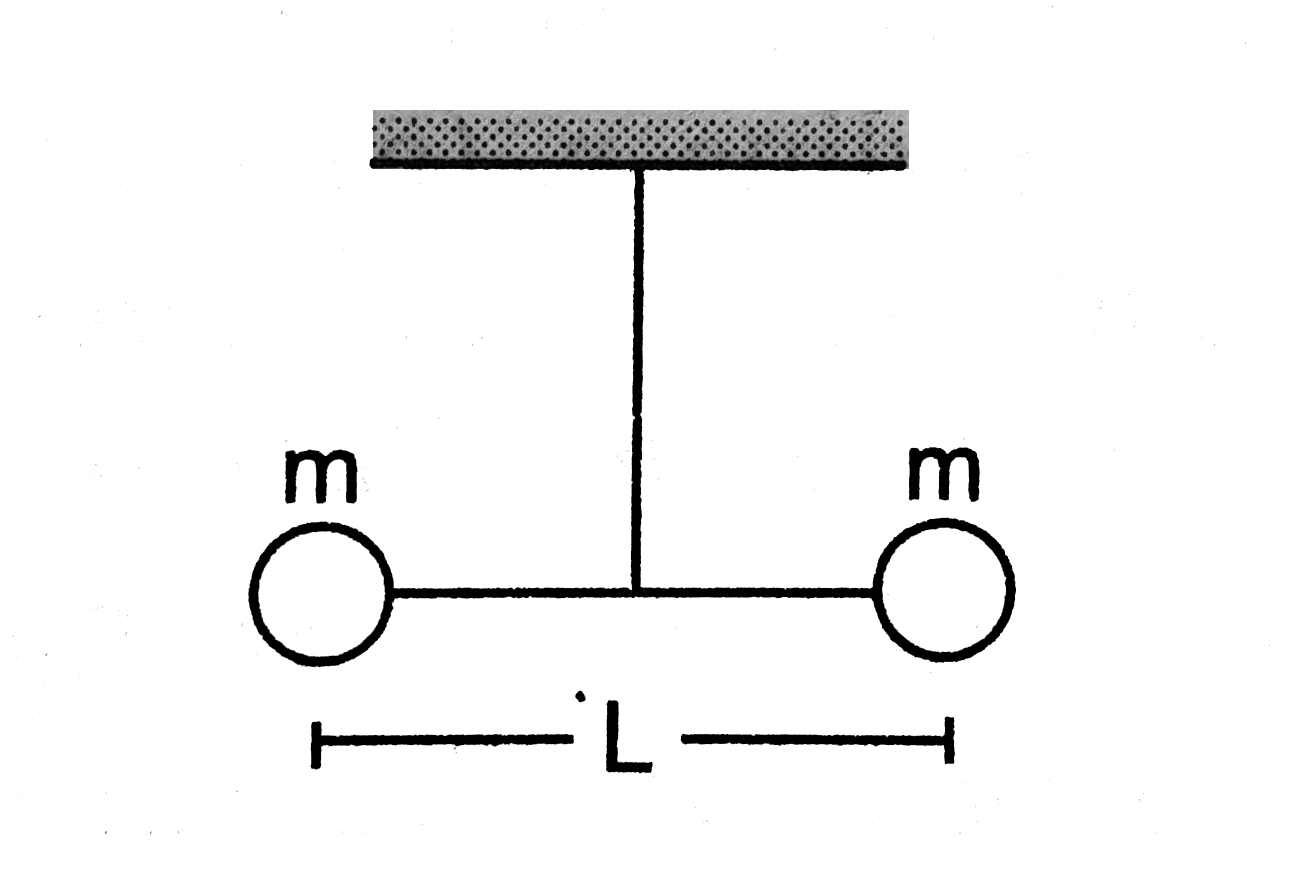
- Two small balls, each of mass m are connected by a light rigid rod of ...
Text Solution
|
- A particle is subjected to two simple harmonic motions of same time pe...
Text Solution
|
- Three simple harmonic motions of equal amplitudes A and equal time per...
Text Solution
|
- A particle is subjected to two simple harmonic motions given by x1=2...
Text Solution
|
- A particle is subjected to two simple harmonic motions, one along the ...
Text Solution
|